Cost of Capital Models and methods to estimate the appropriate

Cost of Capital Models and methods to estimate the appropriate r Remember the guiding principle: The r should reflect the riskiness of the cash flows 1

Dividend Growth Model Approach Re (D1/P0) g Typically used for equity Future dividends? Future growth rates? – Analyst forecasts Analyst are optimists! (Realized growth 40-60% lower) – Historical growth rates – Other models 2

Capital Asset Pricing Model (CAPM) Perfect Competition All investors hold the universe of publicly traded assets and have unlimited access to borrowing/lending at the risk-free rate No taxes or transactions costs All investors plan for one identical holding period All investors are mean-variance optimizers All investors have homogeneous expectations 3

Implementing the CAPM Approach Theoretically can be used on any asset (equity, debt, assets, etc.) – typically used on equity Ri Rf Bi(Rm-Rf) – Only systematic risk (beta) is priced in equilibrium Computing the components – Risk-free rate: Treasury rates – Market risk premium: Expected return on broad based index such as the S&P 500 or Wilshire 5000 – Beta Many services estimate equity betas: READ THEIR METHODOLOGIES!!! Estimate with historical equity data 4

How do we estimate CAPM? Expected Return Model (CAPM) Realized Return Model (Index Model) E ( Ri ) rf i [ E (rM ) rf ] Rit rf i i [rMt rf ] eit Rit i i [rMt ] eit 5

Estimation Issues Beta is non-stationary – What estimation period? – How often do you revise? – Beta moves toward one Data Frequency – Daily, Weekly, Monthly? Market portfolio – S&P 500? – Other equity indices? – Other real assets? 6

Return on Debt Opportunity Cost of Debt Financing – Use the YTM of outstanding debt which reflects opportunity cost – Historical borrowing costs are irrelevant – Coupon rate is irrelevant Use credit ratings to estimate cost of debt Find firms with similar debt risk (probability of bankruptcy) 7

Other Asset Pricing Models Many other models both proprietary and scholarly APT: Arbitrage Pricing Theory Fama/French Model – 3 Factor: Market return, small stock versus big stocks and high versus low book/market (value versus growth stocks) – 4 Factor: Additional momentum factor discovered by Carhart 8

Risk is Difficult to Empirically Measure Data is necessary for empirical observations Usually estimate equity betas because of data availability (asset beta is difficult to observe) Equity risk comparables are difficult to find – Need to have the same capital structure Adjust for different capital structure by levering and unlevering beta – Need to have the same business (asset) risk Industry Estimation: May use industry mean/median Other companies, other projects, divisions, etc. Usually these measures are a combination of asset or business risk and other types of risk (i.e., capital structure) – Adjust by levering and unlevering beta 9

How Do We Manage This Problem? We use the relationship between the total firm market value (V), asset (A), equity (E), debt (D) and the NPV of the capital structure/financing ( ) – Think of the firm value expressed as V A E D – The NPV of the capital structure/financing is the value created by the capital structure choice of the firm In our simple world with no bankruptcy costs, this is basically the tax shield of debt In perfect capital markets NPV of financing is zero (no taxes) The firm (assets) can be viewed as a portfolio of its financing (assume equity, debt and NPV of capital structure/financing) 10

The Relationship The beta of a portfolio is the weighted average of the components therefore E D A E D E D E D E D The return of a portfolio is also the weighted average of the components – Substitute return (r) for beta ( ) in the relationship Note: The use of this relationship is typically called levering and unlevering 11

What is the risk of financing NPV( )? Assume BA B (Case 1) E D A E D E D E D Assume BD B (Case 2) E D A E D E D E D Assume BD B and D (Case 3) E D(1 ) A E D E D(1 ) E D(1 ) 12

Assumptions about NPV of financing ( ) BA B – Asset (business) risk related to the financing risk? More likely if leverage is constant proportion of market value BD B – Debt risk related to the financing risk? More likely if leverage is constant dollar amount Assume BD B and D – Most restrictive assumptions – rd is the appropriate rate, debt is constant dollar amount and a tax deductible perpetuity ( D Drd/rd) How about floating rate debt? Reasonable assumptions? 13

Additional Assumptions What is the beta of debt? – Can we assume it is zero? – If the firm has fixed rate debt and a low probability of bankruptcy, its very close to zero Rule of thumb: Keep the assumptions to a minimum, in other words, lever and unlever only when necessary! 14

Computing An Asset Beta Asset beta is usually difficult to observe How do we estimate an asset beta? – Strip out the asset risk by unlevering the beta – Or find an all equity (pure play) firm Find the Beta for a new hotel project. The industry Be is 1.5%, average industry debt level is 20% and Bd is 0.2%. (assume Case 1). Assume Rf is 3% and Rm is 13%. Does this relationship hold for R also? E D A E D E D E D A 0.8(1.5) 0.2(0.2) A 1.24 R A 0.03 1.24(0.13 0.03) R A 0.1540 E D RA RE RD E D E D RA 0.8(0.18) 0.2(0.05) RA 0.1540 15

Estimate return on equity for a new capital structure Use when you can reasonably estimate New capital structure Changes in cost of debt From the previous example, the industry Ra is 15.4%. Your hotel project is going to have a debt level of 40% and the Rd is 7%. What is your Re? D rE rA (rA rD ) E 4 rE 0.154 (0.154 0.07) 6 rE 0.2100 16

“Whole Firm” Risk Measures From portfolio theory – Portfolio risk is the weighted average of the components’ risk – Works with beta and return (but not volatility) Think of the “whole firm” as components of. – Financing: Debt, equity, other financing (i.e., WACC) – Value: Business (unlevered) and financing flows – Other logical breakouts? Divisions/business units Assets in place and growth opportunities Look to the available data and logical economic components – Used for any complex asset (does not have to be “whole firm”) 17

Weighted Average Cost of Capital When is WACC the appropriate discount rate? – Proposed investment project is similar to the overall business activities of the firm – Project is financed with same capital structure weights as the firm Target weights versus actual weights Represents cost of the next dollar a firm would raise – Simplify the capital structure to debt and equity View the firm as a portfolio of securities – Cost of Equity – Cost of Debt WACC reflects average riskiness of firm's securities 18

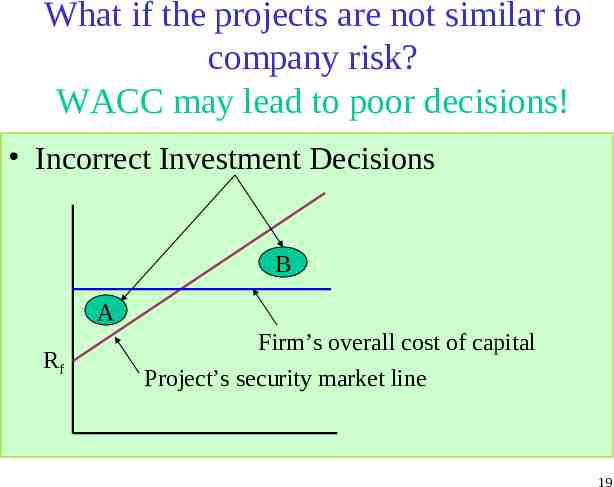
What if the projects are not similar to company risk? WACC may lead to poor decisions! Incorrect Investment Decisions B A Rf Firm’s overall cost of capital Project’s security market line 19

Weighted Average Cost of Capital (WACC) Capital Structure weights (portfolio weights) Use market values WACC (not adjusted) value-weighted average of cost of capital WACC (E/V)Re (D/V)Rd WACC (adjusted) value-weighted average of after tax cost of capital Tax-Advantage of Debt Implies: WACC (E/V)Re [(D/V)Rd*(1- c)] Estimates of Corporate tax rate? 20

Bringing it all together: Cash flow and r? FCF using WACC – Cash flows are the flows to the total firm – WACC is based on the firm’s existing capital structure (RHS of the balance sheet) Adjusted Present Value (APV) – Most common use: Break the flows into flows to assets and flows to financing – NPV plus PV (other benefits or costs) Flow to Equity Approach (FTE) – Only estimate the flows to the equity holders – The appropriate r is the return on equity. 21

Comparison of 3 methods Assume the project is financed with 50 of debt which costs 8% and 50 of equity which costs 12%. The yearly perpetual project cash flow is 8.8, the tax rate is 30% and assume you can perpetually take advantage of the tax shield of debt. What is the NPV? 22

WACC 50 50 WACC 0.12 0.08(1 0.3) 0.088 100 100 8.8 NPV 100 0 0.088 FTE – Equity income cash flow minus after tax cost of debt Exp (equityincome) C DrD (1 C ) 8.8 (50)(0.08)(1 0.3) 6 6 NPV 50 0 0.12 23

APV: One approach (r based on who receives flow) 50 50 WACC (notaxes) 0.12 0.08 0.1 100 100 Cashflow(debttaxshield ) (50)(0.08)(0.3) 1.2 8.8 1.2 APV 100 0 0.1 0.1 Second approach (r based on origin of flow) D rE ra (1 c )(ra rD ) E 50 0.12 ra (1 0.3)(ra 0.08) 50 ra 0.1035 NPV 100 8.8 1.2 0 0.1035 0.08 24