Computer Networks CMSC 417 : Spring 2020 Topic:

Computer Networks CMSC 417 : Spring 2020 Topic: Internetworking (Textbook chapter 3) Nirupam Roy Tu-Th 2:00-3:15pm CSI 1115

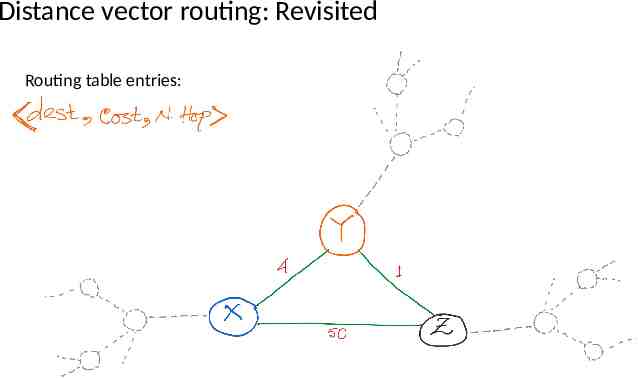
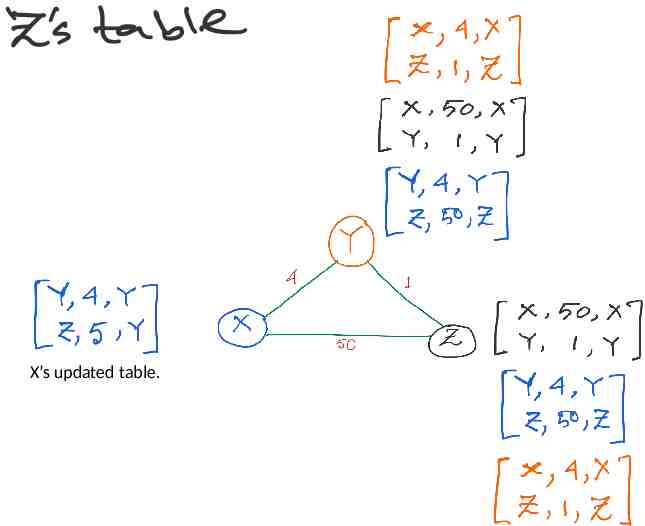
Distance vector routing: Revisited Routing table entries:

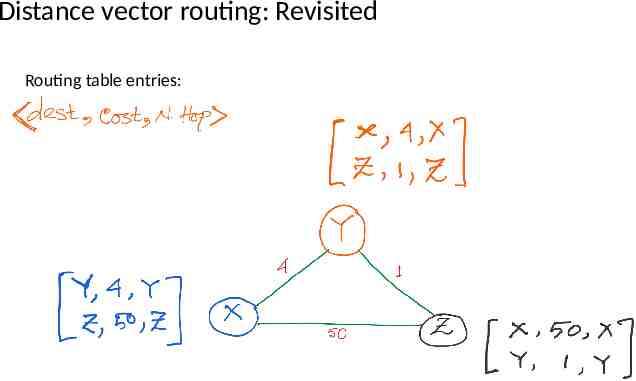
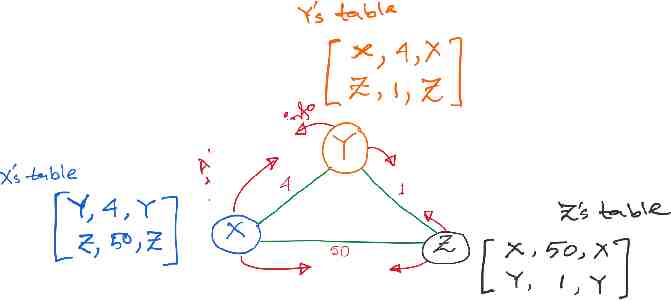
Distance vector routing: Revisited Routing table entries:

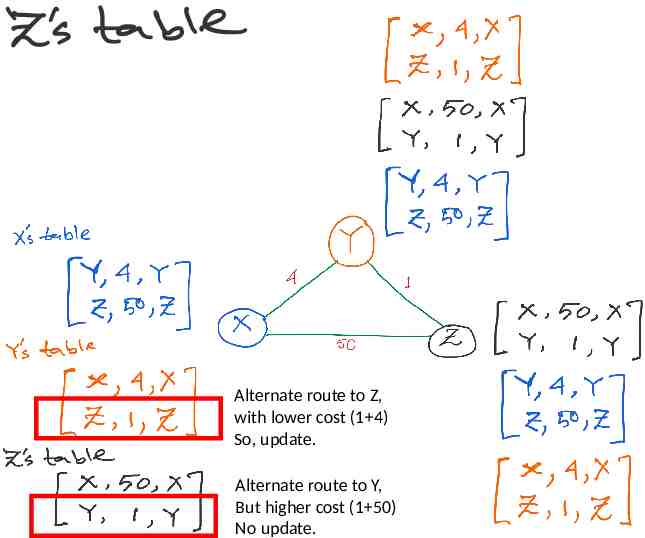
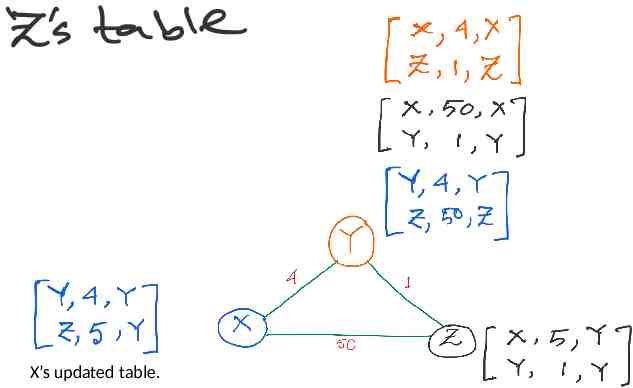
Alternate route to Z, with lower cost (1 4) So, update. Alternate route to Y, But higher cost (1 50) No update.

X’s updated table.

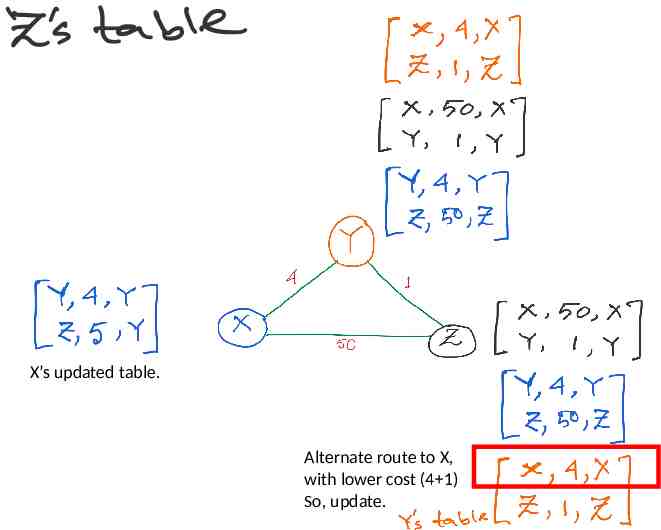
X’s updated table. Alternate route to X, with lower cost (4 1) So, update.

X’s updated table.

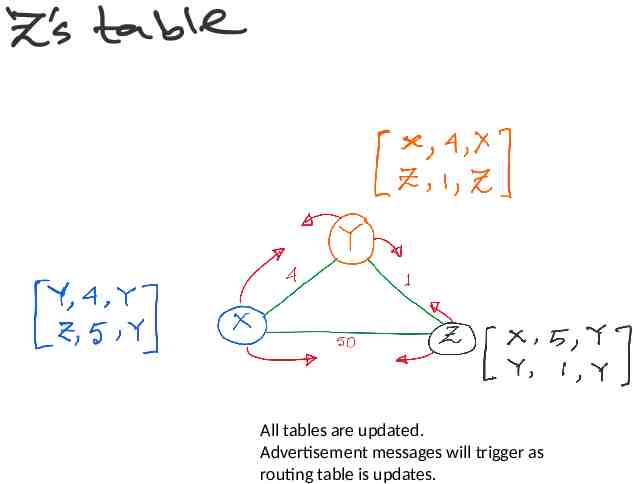
All tables are updated. Advertisement messages will trigger as routing table is updates.

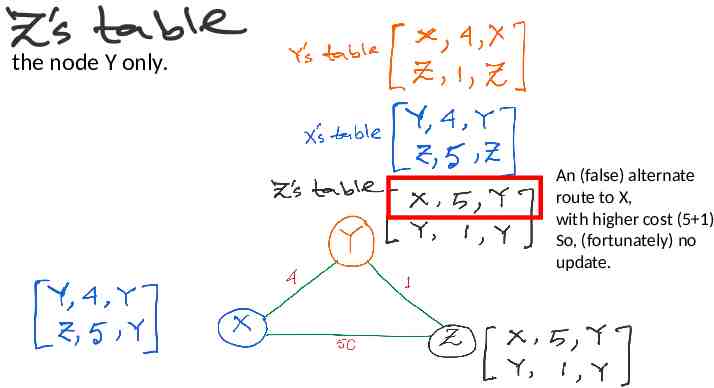
Let’s take a look at the node Y only. An (false) alternate route to X, with higher cost (5 1) So, (fortunately) no update.

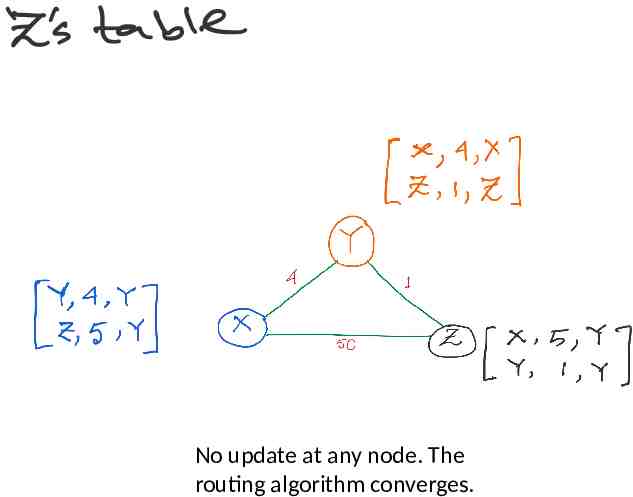
No update at any node. The routing algorithm converges.

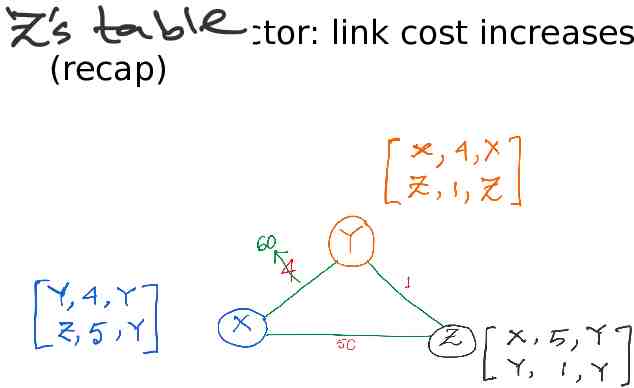
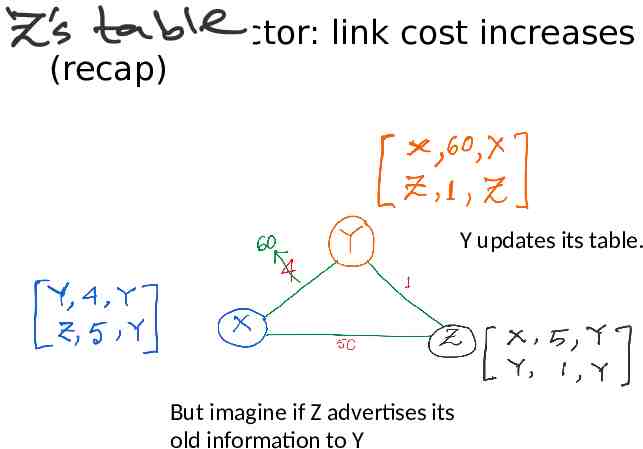
Distance vector: link cost increases (recap)

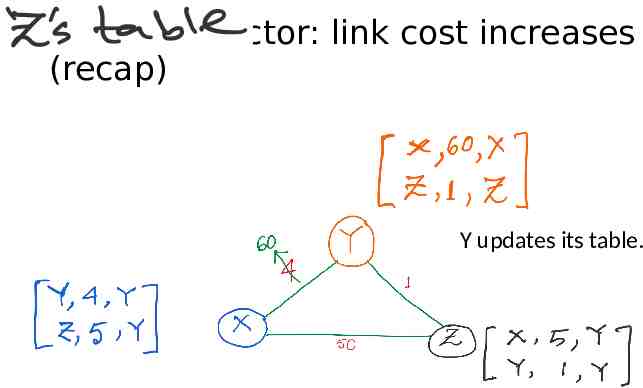
Distance vector: link cost increases (recap) Y updates its table.

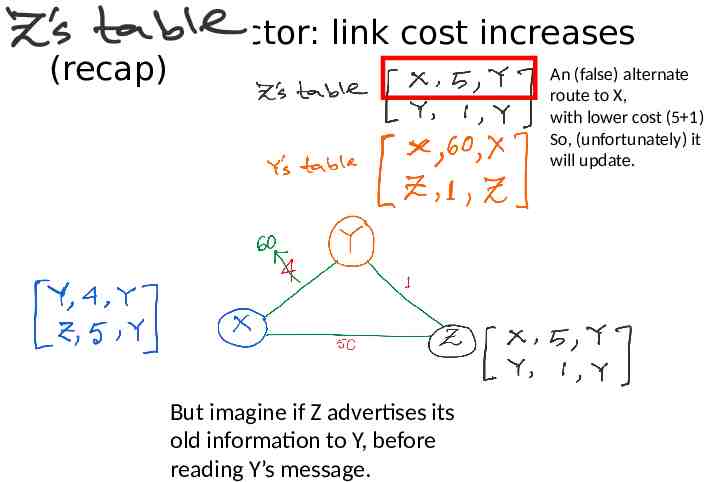
Distance vector: link cost increases (recap) Y updates its table. But imagine if Z advertises its old information to Y

Distance vector: link cost increases An (false) alternate (recap) route to X, with lower cost (5 1) So, (unfortunately) it will update. But imagine if Z advertises its old information to Y, before reading Y’s message.

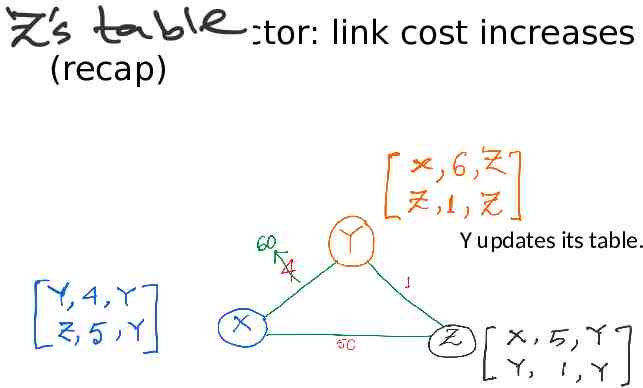
Distance vector: link cost increases (recap) Y updates its table.

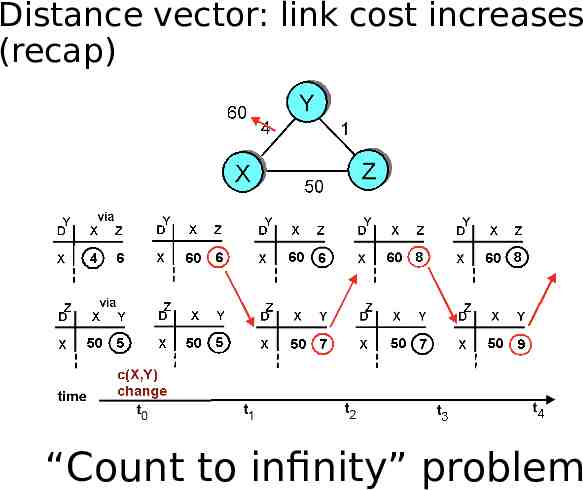
Distance vector: link cost increases (recap) “Count to infinity” problem

Count-to-infinity Problem Use some relatively small number as an approximation of infinity For example, the maximum number of hops to get across a certain network is never going to be more than 16 One technique to improve the time to stabilize routing is called split horizon When a node sends a routing update to its neighbors, it does not send those routes it learned from each neighbor back to that neighbor For example, if B has the route (E, 2, A) in its table, then it knows it must have learned this route from A, and so whenever B sends a routing update to A, it does not include the route (E, 2) in that update

Count-to-infinity Problem In a stronger version of split horizon, called split horizon with poison reverse B actually sends that back route to A, but it puts negative information in the route to ensure that A will not eventually use B to get to E For example, B sends the route (E, ) to A

Distance vector: Poisoned reverse Does poison reverse solve the general count-to-infinity problem? It does not. It may be possible that loops involving three or more nodes (rather than simply two immediately neighboring nodes, as we shown in last example) will not be detected by the poison reverse technique.

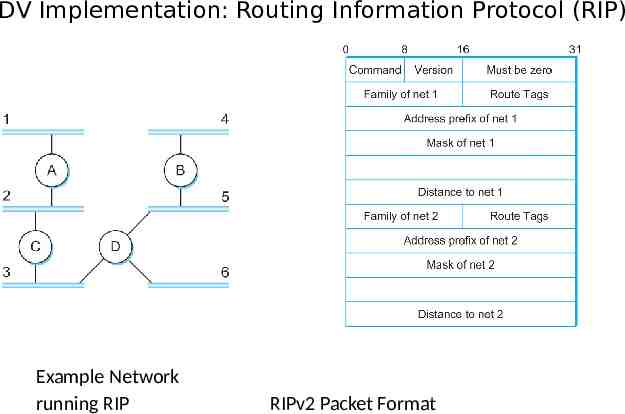
DV Implementation: Routing Information Protocol (RIP) Example Network running RIP RIPv2 Packet Format

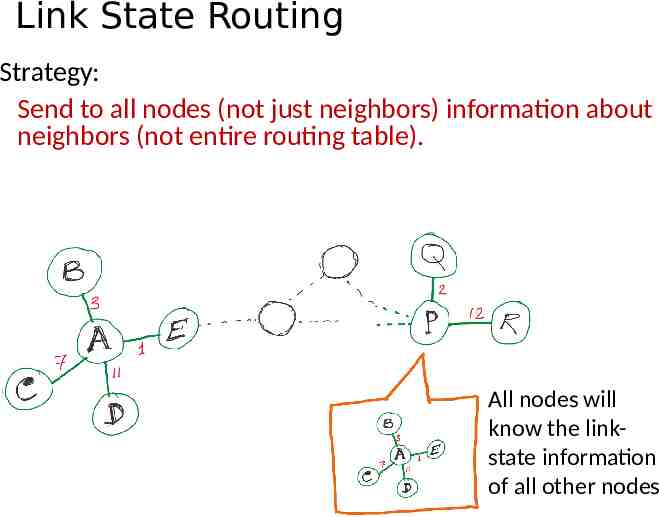
Link State Routing

Link State Routing Strategy: Send to all nodes (not just neighbors) information about neighbors (not entire routing table). All nodes will know the linkstate information of all other nodes

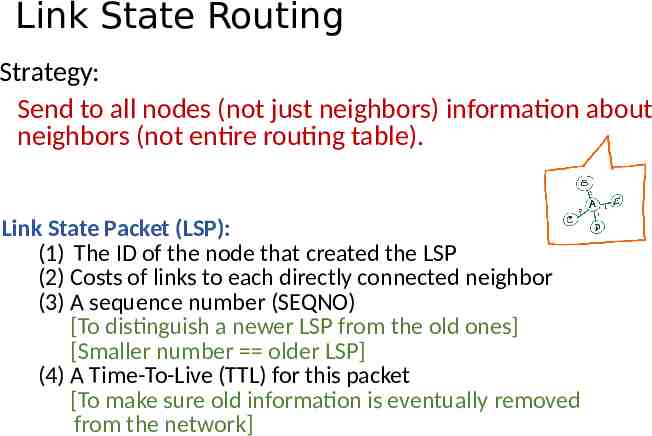
Link State Routing Strategy: Send to all nodes (not just neighbors) information about neighbors (not entire routing table). Link State Packet (LSP): (1) The ID of the node that created the LSP (2) Costs of links to each directly connected neighbor (3) A sequence number (SEQNO) [To distinguish a newer LSP from the old ones] [Smaller number older LSP] (4) A Time-To-Live (TTL) for this packet [To make sure old information is eventually removed from the network]

Link State Routing (1) Reliable flooding [Makes sure all nodes in the network get a copy of LSP from all other nodes] (2) Route calculation (Dijkstra’s shortest path algorithm) [Calculates the shortest path from each node to all other nodes and the corresponding nexthop]

Link State Routing: Reliable flooding Store most recent LSP from each node Forward LSP to all nodes but one that sent it Generate new LSP periodically; increment SEQNO Start SEQNO at 0 when reboot Decrement TTL before flooding it to neighbors. Also age the stored LSP (decrement TTL) Discard when TTL 0. Goals: 1) Flood in minimum time 2) Minimize total routing traffic

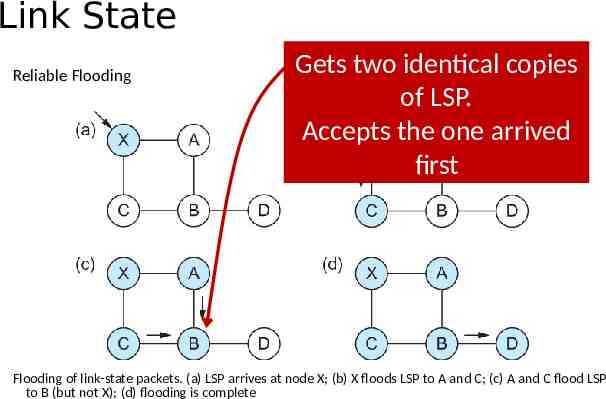
Link State Reliable Flooding Gets two identical copies of LSP. Accepts the one arrived first Flooding of link-state packets. (a) LSP arrives at node X; (b) X floods LSP to A and C; (c) A and C flood LSP to B (but not X); (d) flooding is complete

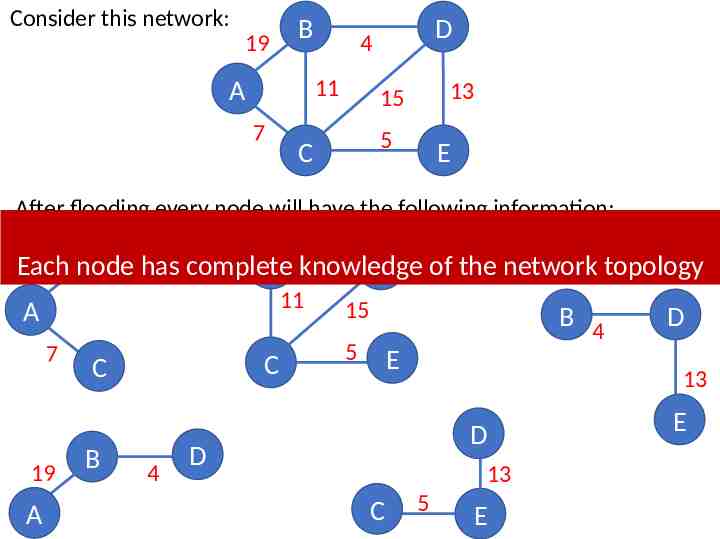
Consider this network: 19 B 4 11 A 7 D 13 15 5 C E After flooding every node will have the following information: B has complete 19 node B knowledge Each D of the network topology 11 A 7 19 A C C B 4 15 B 4 5 E 13 D D 13 C D 5 E E

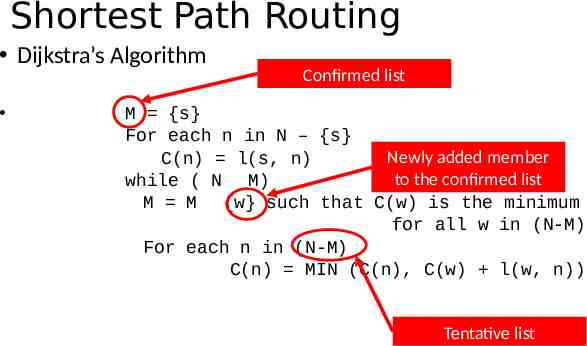
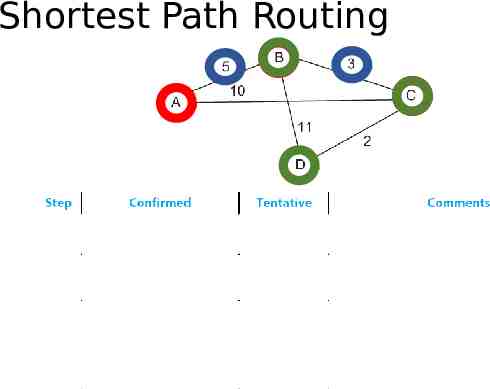
Shortest Path Routing Dijkstra’s Algorithm - Assume non-negative link weights N: set of nodes in the graph l((i, j): the non-negative cost associated with the edge between nodes i, j N and l(i, j) if no edge connects i and j Let s N be the starting node which executes the algorithm to find shortest paths to all other nodes in N Two variables used by the algorithm M: set of nodes incorporated so far by the algorithm C(n) : the cost of the path from s to each node n The algorithm M {s} For each n in N – {s} C(n) l(s, n) while ( N M) M M {w} such that C(w) is the minimum for all w in (N-M) For each n in (N-M) C(n) MIN (C(n), C(w) l(w, n))

Shortest Path Routing In practice, each switch computes its routing table directly from the LSP’s it has collected using a realization of Dijkstra’s algorithm called the forward search algorithm Specifically each switch maintains two lists, known as Tentative and Confirmed Each of these lists contains a set of entries of the form (Destination, Cost, NextHop)

Shortest Path Routing Dijkstra’s Algorithm Confirmed list M {s} For each n in N – {s} Newly added member C(n) l(s, n) to the confirmed list while ( N M) M M {w} such that C(w) is the minimum for all w in (N-M) For each n in (N-M) C(n) MIN (C(n), C(w) l(w, n)) Tentative list

Shortest Path Routing The algorithm Initialize the Confirmed list with an entry for myself; this entry has a cost of 0 For the node just added to the Confirmed list in the previous step, call it node Next, select its LSP For each neighbor (Neighbor) of Next, calculate the cost (Cost) to reach this Neighbor as the sum of the cost from myself to Next and from Next to Neighbor If Neighbor is currently on neither the Confirmed nor the Tentative list, then add (Neighbor, Cost, Nexthop) to the Tentative list, where Nexthop is the direction I go to reach Next If Neighbor is currently on the Tentative list, and the Cost is less than the currently listed cost for the Neighbor, then replace the current entry with (Neighbor, Cost, Nexthop) where Nexthop is the direction I go to reach Next If the Tentative list is empty, stop. Otherwise, pick the entry from the Tentative list with the lowest cost, move it to the Confirmed list, and return to Step 2.

Shortest Path Routing

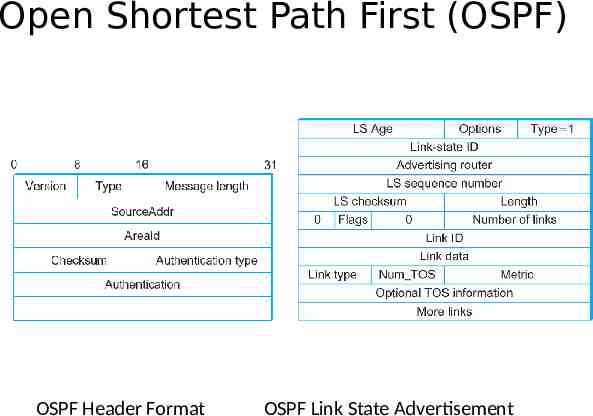
Open Shortest Path First (OSPF) OSPF Header Format OSPF Link State Advertisement

Comparison of LS and DV algorithms message complexity LS: with n nodes, E links, O(nE) msgs sent DV: exchange between neighbors only convergence time varies speed of convergence LS: O(n2) algorithm requires O(nE) msgs may have oscillations DV: convergence time varies may be routing loops count-to-infinity problem robustness: what happens if router malfunctions? LS: node can advertise incorrect link cost each node computes only its own table DV: DV node can advertise incorrect path cost each node’s table used by others error propagate thru network 35