Column Generation Jacques Desrosiers Ecole des HEC & GERAD

Column Generation Jacques Desrosiers Ecole des HEC & GERAD

Contents The Cutting Stock Problem Basic Observations LP Column Generation Dantzig-Wolfe Decomposition Dantzig-Wolfe decomposition vs Lagrangian Relaxation Equivalencies Alternative Formulations to the Cutting Stock Problem IP Column Generation Branch-and- . Acceleration Techniques Concluding Remarks COLUMN GENERATION 2

A Classical Paper : The Cutting Stock Problem P.C. Gilmore R.E. Gomory & I : set of items ni : number of times item i is requested A Linear Programming Approach to the Cutting Stock Problem. Oper. Res. 9, 859. (1960) 849- : length of item i L : length of a standard li roll J : set of cutting patterns aij : number of times item i Yj is cut in pattern j : number of times pattern j is used COLUMN GENERATION 3

The Cutting Stock Problem . Set P : min Y j j J aijY j ni , i I j J Y j 0, Yj integer, j J j J J can be huge. Solution ofLP, P, the linear relaxation of by column generation. LP : min Y j j J a Y ij Minimize the number of standard rolls used j ni , i I j J Y j 0, j J COLUMN GENERATION 4

The Cutting Stock Problem . Given a subset J ' J and the dual multipliers i LP : min Y j j J a Y ij j ni , i I j J Y j 0, j J i ( J ' ), i I , the reduced cost of any new patterns must satisfy: min 1 j J \ J ' otherwise, optimal. a ij i I LP i 0; is COLUMN GENERATION 5

The Cutting Stock Problem . Reduced costs forj J ' are non negative, hence: min 1 i aij j J \ J ' min j J min i I 1 i i aij i I 1 ai i I l a i i L i I ai 0 integer, i I ai is a decision variable: the number of times item i is selected in a new pattern. The Column Generator max is ai ai I Knapsacki Problem. li ai L i I ai 0 integer, i I COLUMN GENERATION 6

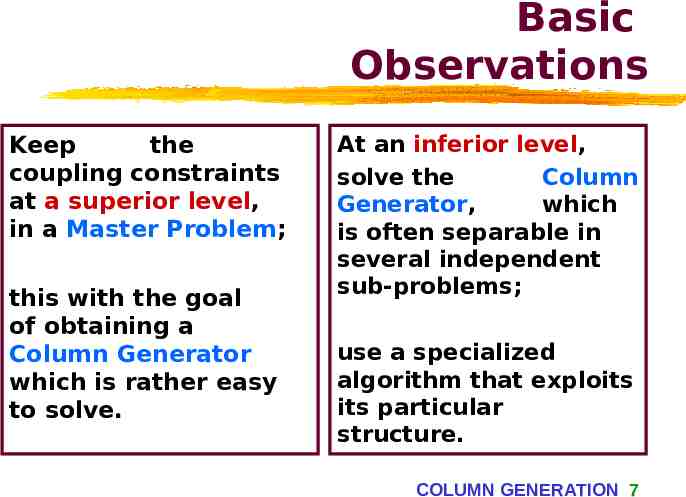
Basic Observations Keep the coupling constraints at a superior level, in a Master Problem; this with the goal of obtaining a Column Generator which is rather easy to solve. At an inferior level, solve the Column Generator, which is often separable in several independent sub-problems; use a specialized algorithm that exploits its particular structure. COLUMN GENERATION 7

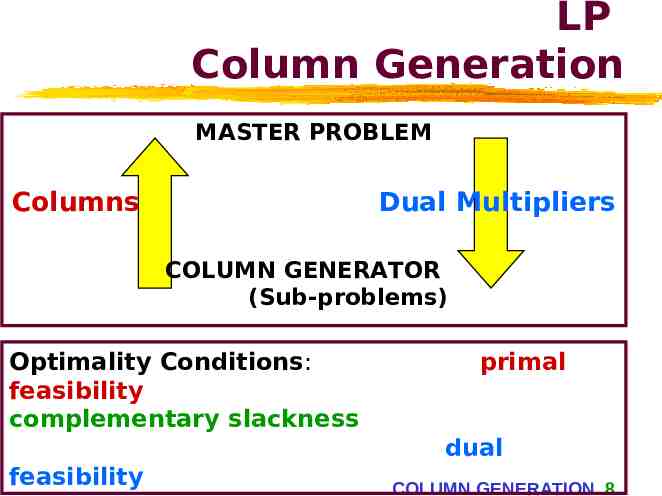
LP Column Generation MASTER PROBLEM Columns Dual Multipliers COLUMN GENERATOR (Sub-problems) Optimality Conditions: feasibility complementary slackness primal dual feasibility COLUMN GENERATION 8

Historical Perspective G.B. Dantzig P. Wolfe & Decomposition Principle for Linear Programs. Oper. Res. 8, 111. (1960) Authors give credit to: L.R. Ford & D.R. Fulkerson A Suggested Computation for Multicommodity flows. 101Man. Sc. 5, (1958) 97-101. COLUMN GENERATION 9

Historical Perspective : a Dual Approach DUAL MASTER PROBLEM Rows Dual Multipliers ROW GENERATOR J.E. Kelly (Sub-problems) The Cutting Plane Method for Solving Convex Programs. SIAM 8, 703-712. (1960) COLUMN GENERATION 10

Dantzig-Wolfe Decomposition : the Principle P : min cx Ax b x X On conv( X ), define sets ( ) : extreme points ( ) : extreme rays x Conv ( X ) rewritten as : x x p p p ( ) p d r r r ( ) 1 p ( ) p 0, p ( ) r 0, r ( ) COLUMN GENERATION 11

Dantzig-Wolfe Decomposition : Substitution P : min cx Ax b x X P : min c( x p p p ( ) A( r r r ( ) x p p p ( ) d ) d ) b r r r ( ) p 1 p ( ) p 0, p ( ) r 0, r ( ) COLUMN GENERATION 12

Dantzig-Wolfe Decomposition : The Master Problem P : min c( x p p p ( ) A( r r d ) b r r r ( ) p P : min r ( ) x p p p ( ) d ) 1 The Master Problem p ( ) (cd ) r r r ( ) ( Ax p ) p p ( ) ( Ad ) r r b r ( ) p ( ) (cx p ) p p 1 p ( ) p 0, p ( ) p 0, p ( ) r 0, r ( ) r 0, r ( ) COLUMN GENERATION 13

Dantzig-Wolfe Decomposition : The Column Generator Given the current dual multipliers for a subset of columns : coupling constraints convexity constraint ( ) generate (if possible) o new columns with negative reduced cost : min cx ( Ax) 0 x conv( X ) extreme rays if (c A)d r 0, for some r ( ) otherwise extreme points if cx p ( Ax p ) 0 0, for some p ( ) COLUMN GENERATION 14

Remark extreme rays if extreme rays if (c A)d r 0, (c A)d r 0, for some r ( ) for some r ( ) otherwise extreme points if otherwise extreme points if cx p ( Ax p ) 0 0, cx p ( Ax p b) b 0 , for some p ( ) for some p ( ) COLUMN GENERATION 15

Dantzig-Wolfe Decomposition : Block Angular Structure P : min c k x k k K k A x k b k K k k x X , k K Exploits the structure of many sub-problems. Similar developments & results. COLUMN GENERATION 16

Dantzig-Wolfe Decomposition : Algorithm MASTER PROBLEM Columns COLUMN GENERATOR Optimality Conditions: feasibility complementary slackness Dual Multipliers (Sub-problems) primal dual feasibility COLUMN GENERATION 17

Dantzig-Wolfe Decomposition : a Lower Bound Given the current dual multipliers ( ) o (coupling constraints) (convexity constraint), a lower bound can be computed at each iteration, as follows: Current solution value minimum reduced cost column (b 0 ) min cx ( Ax) 0 x X min cx ( Ax b) x X COLUMN GENERATION 18

Lagrangian Relaxation Computes the Same Lower Bound P : min cx Ax b x X L( ) min cx ( Ax b) x conv( X ) provides a lower bound on P : if (c A)d r 0, for some r ( ) ; cx p ( Ax p b) for some p ( ), otherwise. The best lower bound is obtained using max L( ). COLUMN GENERATION 19

Dantzig-Wolfe vs Lagrangian Decomposition Relaxation Essentially utilized for Linear Programs Essentially utilized for Integer Programs Relatively difficult to implement Easy to implement with subgradient adjustment for multipliers Slow convergence No stopping rule ! Rarely implemented 6% of OR papers COLUMN GENERATION 20

Equivalencies Dantzig-Wolfe Decomposition & Lagrangian Relaxation if both have the same sub-problems In both methods, coupling or complicating constraints go into a DUAL MULTIPLIERS ADJUSTMENT PROBLEM : in DW : a LP Master Problem in Lagrangian Relaxation : max L( ) COLUMN GENERATION 21

Equivalencies . Column Generation corresponds to the solution process used in Dantzig-Wolfe decomposition. This approach can also be used directly by formulating a Master Problem and sub-problems rather than obtaining them by decomposing a Global formulation of the problem. However . COLUMN GENERATION 22

Equivalencies . for any Column Generation scheme, there exits a Global Formulation that can be decomposed by using a generalized Dantzig-Wolfe decomposition which results in the same Master and subproblems. The definition of the Global Formulation is not unique. A nice example: The Cutting Stock Problem COLUMN GENERATION 23

The Cutting Stock Problem : Kantorovich (1960/1939) K : set of available rolls Y min Y k K k X i n i , k : binary variable, 1 if roll k is cut, 0 otherwise X i I k K k k l X L Y , k K i i i I k i : number of times item i is cut on roll k k k Y 0 or 1, k K k i X 0 integer, i I , k K . COLUMN GENERATION 24

The Cutting Stock Problem : Kantorovich . Kantorovich’s LP lower bound is weak: l n i i I i / L. However, DantzigWolfe decomposition provides the same bound as the GilmoreGomory LP bound if sub-problems are solved as . K integer Knapsack Problems, (which provide extreme point columns). Aggregation of identical columns in the Master Problem. Branch & Bound k performed on X i . COLUMN GENERATION 25

The Cutting Stock Problem : Valerio de Carvalhó (1996) ( N , A) Network type formulation on graph N {0, 1, 2,., L 1, L} A {(u , v) : 0 u v L and v u li , i I } {(u, u 1), u 0,1,., L 1} Example with L 5 , and l1 2, l2 3 COLUMN GENERATION 26

The Cutting Stock Problem : Valerio de Carvalhó . min X ( u ,u li ) A u , u li X Z n i , 0v i I z, ( 0 ,v ) X ( u ,v ) uv X vu 0, X uL z, v {1, 2 , , L 1} ( v ,u ) (u , L ) X uv 0 integer, (u , v ) A COLUMN GENERATION 27

The Cutting Stock Problem : Valerio de Carvalhó . The sub-problem is a shortest path problem on a acyclic network. The Master Problem appears without the convexity constraint. This Column Generator only brings back extreme ray columns, the single extreme point being the null vector. The correspondence with Gilmore-Gomory formulation is obvious. Branch & Bound performed on X uv . COLUMN GENERATION 28

The Cutting Stock Problem : Desaulniers et al. (1998) It can also be viewed as a Vehicle Routing Problem on a acyclic network (multicommodity flows): Vehicles Customers Demands Capacity Rolls Items li ni L Column Generation tools developed for Routing Problems can be used. Columns correspond to paths visiting items the requested number of times. Branch & Bound k performed on X ij . COLUMN GENERATION 29

IP Column Generation IP : min x X x integer (cx p ) p p ( ) IP : min cx Ax b (cd ) r r r ( ) ( Ax p ) p p ( ) ( Ad ) r r b r ( ) p 1 p ( ) p 0, p ( ) r 0, r ( ) x x p p ( ) p d r r r ( ) x integer COLUMN GENERATION 30

Integrality Property The sub-problem satisfies the Integrality Property if it has an integer optimal solution for any choice of linear objective function, even if the integrality restrictions on the variables are relaxed. In this case, max L( ) v( LP ) otherwise v( LP ) max L( ) v( IP) i.e., the solution process partially explores the integrality gap. COLUMN GENERATION 31

Integrality Property . In most cases, the Integrality Property is a undesirable property! Exploiting the non trivial integer structure reveals that . some overlooked formulations become very good when a Dantzig-Wolfe decomposition process is applied to them. The Cutting Stock Problem Localization Problems Vehicle Routing Problems . COLUMN GENERATION 32

IP Column Generation : Branch-and-. Branch-and-Bound : Branch-and-Cut : branching decisions on a combination of the original (fractional) variables cutting planes defined on a combination of the original variables; of a Global Formulation on which Dantzig-Wolfe Decomposition is applied. at the Master level, as coupling constraints; in the sub-problem, as local constraints. COLUMN GENERATION 33

IP Column Generation : Branch-and-. IP : min c x Ax b x X x integer { Branching Cutting decisions & } Dantzig-Wolfe decomposition applied at all decision nodes COLUMN GENERATION 34

IP Column Generation: Branch-and-. Branch-and-Price : a nice name which hides a well known solution process relatively easy to apply. For alternative methods, see the work of S. Holm & J. Tind C. Barnhart, E. Johnson, G. Nemhauser, P. Vance, M. Savelsbergh, . F. Vanderbeck & L. Wolsey COLUMN GENERATION 35

Application to Vehicle Routing and Crew Scheduling Problems (1981 - ) J. Desrosiers, Y. Dumas, F. Soumis & M. Solomon Time Constrained Routing and Scheduling Handbooks in OR & MS, 8 (1995) G. Desaulniers et al. A Unified Framework for Deterministic Vehicle Routing and Crew Scheduling Problems T. Crainic & G. Laporte (eds) Fleet Management & Logistics (1998) Global Formulation : Non-Linear Integer Multi-Commodity Flows Master Problem : Covering & Other Linking Constraints Column Generator : Resource Constrained Shortest Paths COLUMN GENERATION 36

Resource Constrained Shortest Path Problem on G (N,A) Min c x T ij ij P(N, A) : ij j:( i , j ) A x ij j:( j ,i ) A i i i N r R ( i , j ) A x r 1, i o; 1, i d ; 0, i o, d xij ( f ij (Ti ) T jr ) 0, (i, j ) A, r R ( r r x ) a T ij i i ( j:( i , j ) A r x ) b ij i , i N , r R j:( i , j ) A xij binary, (i, j ) A COLUMN GENERATION 37

Integer Multi-Commodity Network Flow Structure Min k k ij ij ( c k K ( ( k x ij ) bi , j:( i , j ) Ak k K k K ( i , j ) A k k kr i i x T ) i N k r R i N k k K k k kr kr a x a m,ij ij m,iTi ) bm , m M ( i , j ) Ak i N k ( x k , T k ) P( N k , Ak ), k K COLUMN GENERATION 38

Vehicle Routing and Crew Scheduling Problems . Sub-Problem strongly NP-hard is It does not posses the Integrality Property Master Problem results in Set Partitioning/Covering type Problems Paths Extreme points Branching and Cutting decisions are taken on the original network flow, resource and supplementary variables COLUMN GENERATION 39

IP Column Generation : Acceleration Techniques Exploit all the Structures on the Column Generator With Fast Heuristics Master Problem Re-Optimizers Global Formulation Pre-Processors To get Primal & Dual Solutions COLUMN GENERATION 40

IP Column Generation : Acceleration Techniques . Link all the Structures Multiple Columns : selected subset close to expected optimal solution Partial Pricing in case of many Sub-Problems : as in the Simplex Method Early & Multiple Branching & Cutting : quickly gets local optima Be Innovative ! Primal Perturbation & Dual Restriction : to avoid degeneracy and convergence difficulties Branching & Cutting : on integer variables ! Branch-first, Cut-second Approach : exploit solution structures COLUMN GENERATION 41

Stabilized Column Generation min cx Ax y1 y2 b x 0 0 y1 1 ,0 y2 2 Perturbed Primal min cx Ax b x 0 max b max b A c A c d1 d 2 min cx d1 y1 d 2 y 2 Restricted Dual Ax y1 y 2 b x 0 0 y1 1 , 0 y 2 2 Stabilized Problem COLUMN GENERATION 42

Concluding Remarks DW Decomposition is an intuitive framework that requires all tools discussed to become applicable “easier” for IP very effective in several applications Imagine what could be done with theoretically better methods such as the Analytic Center Cutting Plane Method (Vial, Goffin, du Merle, Gondzio, Haurie, et al.) which exploits recent developments in interior point methods, and is also compatible with Column Generation. COLUMN GENERATION 43

“Bridging Continents and Cultures” F. Soumis M. Solomon G. Desaulniers P. Hansen J.-L. Goffin O. Marcotte G. Savard O. du Merle O. Madsen P.O. Lindberg B. Jaumard Canada, USA, Italy, Denmark, Sweden, Norway, Ile Maurice, France, Iran, Congo, New Zealand, Brazil, Australia, Germany, Romania, Switzerland, Belgium, Tunisia, Mauritania, Portugal, China, The Netherlands, . M. Desrochers Y. Dumas M. Gamache D. Villeneuve K. Ziarati I. Ioachim M. Stojkovic G. Stojkovic N. Kohl A. Nöu et al. COLUMN GENERATION 44