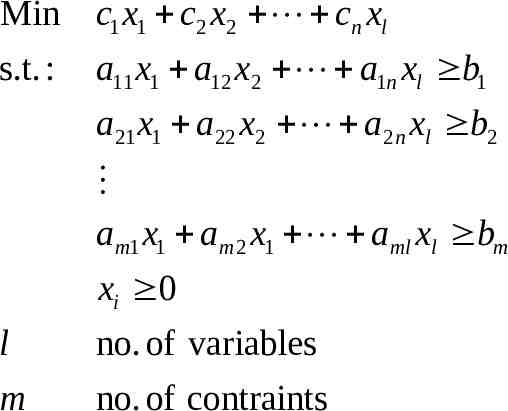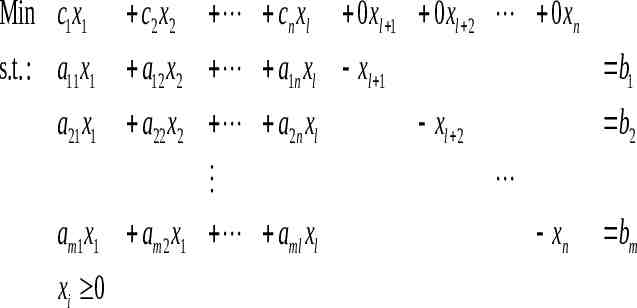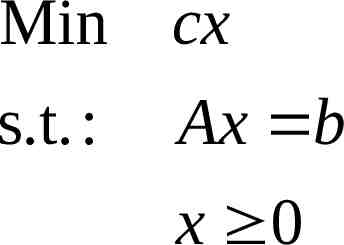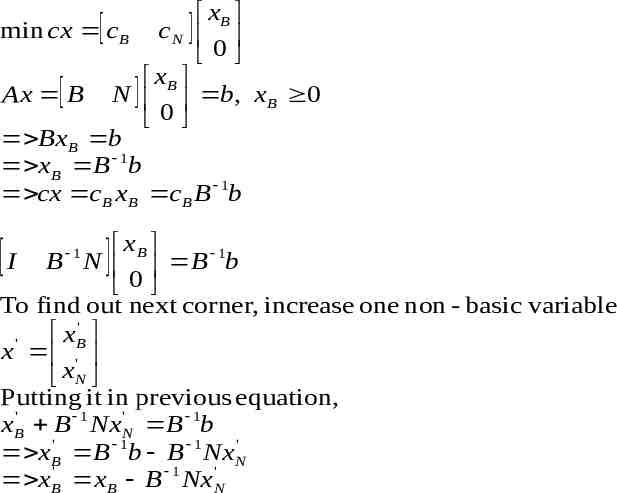Column Generation By Soumitra Pal Under the guidance of Prof. A.

Column Generation By Soumitra Pal Under the guidance of Prof. A. G. Ranade

Agenda Introduction Basics of Simplex algorithm Formulations for the CSP (Delayed) Column Generation Branch-and-price Flow formulation of CSP & solution Conclusions

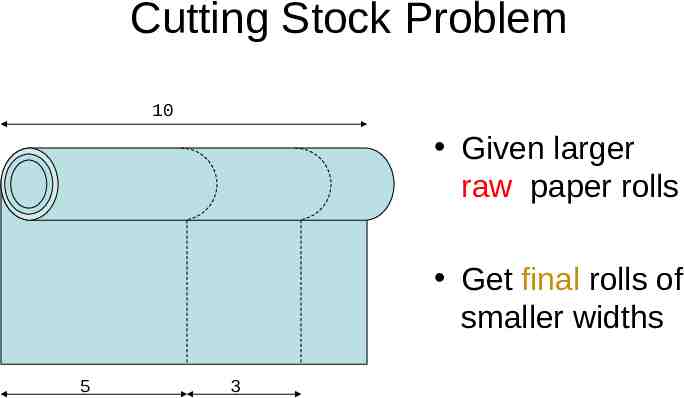
Cutting Stock Problem 10 Given larger raw paper rolls Get final rolls of smaller widths 5 3

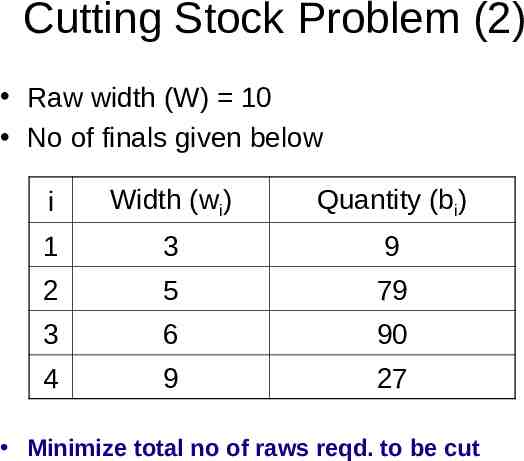
Cutting Stock Problem (2) Raw width (W) 10 No of finals given below i Width (wi) Quantity (bi) 1 3 9 2 5 79 3 6 90 4 9 27 Minimize total no of raws reqd. to be cut

Agenda Introduction Basics of Simplex algorithm Formulations for the CSP (Delayed) Column Generation Branch-and-price Flow formulation of CSP & solution Conclusions

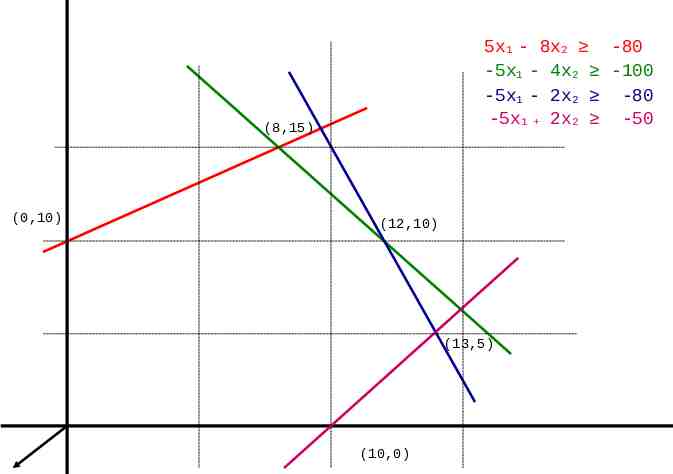
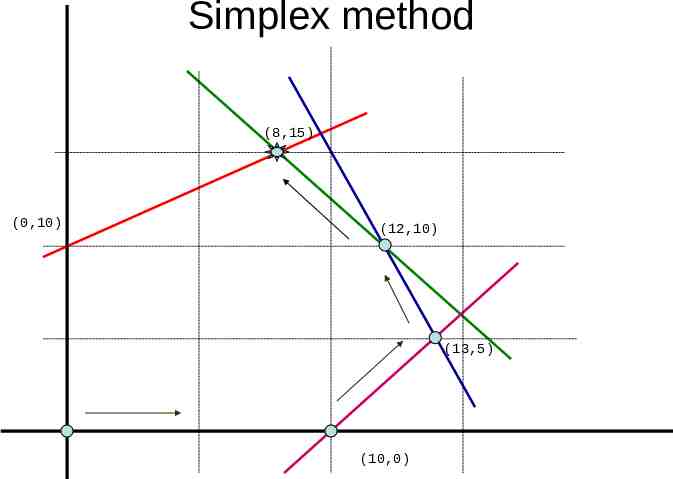
Objective/ Cost fn Constraints Min -x1 -x2 5x1 - 8x2 -80 -5x1 - 4x2 -100 -5x1 - 2x2 -80 -5x1 2x2 -50

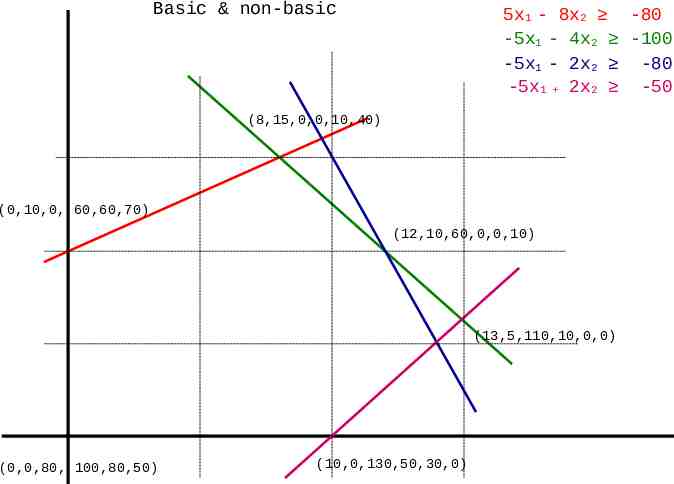
5x1 - 8x2 -80 -5x1 - 4x2 -100 -5x1 - 2x2 -80 -5x1 2x2 -50 (8,15) (0,10) (12,10) (13,5) (10,0)

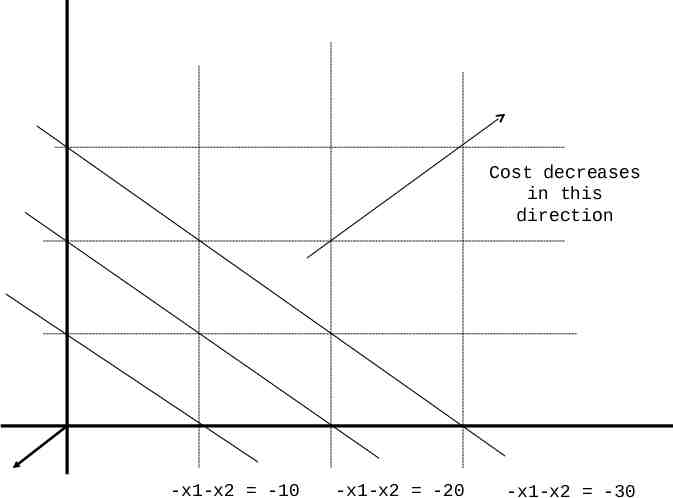
Cost decreases in this direction -x1-x2 -10 -x1-x2 -20 -x1-x2 -30

Simplex method (8,15) (0,10) (12,10) (13,5) (10,0)

Min c1 x1 c2 x2 cn xl s.t. : a11 x1 a12 x2 a1n xl b1 a21 x1 a22 x2 a2 n xl b2 am1 x1 am 2 x1 aml xl bm xi 0 l no. of variables m no. of contraints

Min c1 x1 c2 x2 cn xl 0 xl 1 0 xl 2 0 xn s.t. : a11 x1 a12 x2 a1n xl xl 1 a21 x1 a22 x2 a2n xl am1x1 am2 x1 aml xl xi 0 b1 xl 2 b2 xn bm

Min cx s.t. : Ax b x 0

Basic & non-basic 5x1 - 8x2 -80 -5x1 - 4x2 -100 -5x1 - 2x2 -80 -5x1 2x2 -50 (8,15,0,0,10,40) (0,10,0, 60,60,70) (12,10,60,0,0,10) (13,5,110,10,0,0) (0,0,80, 100,80,50) (10,0,130,50,30,0)

xB min cx c B c N 0 xB Ax B N b, xB 0 0 BxB b xB B 1b cx cB xB cB B 1b xB I B N B 1b 0 To find out next corner, increase one non - basic variable ' x ' B x ' xN Putting it in previous equation, xB' B 1 NxN' B 1b xB' B 1b B 1 NxN' xB' xB B 1 Nx N' 1

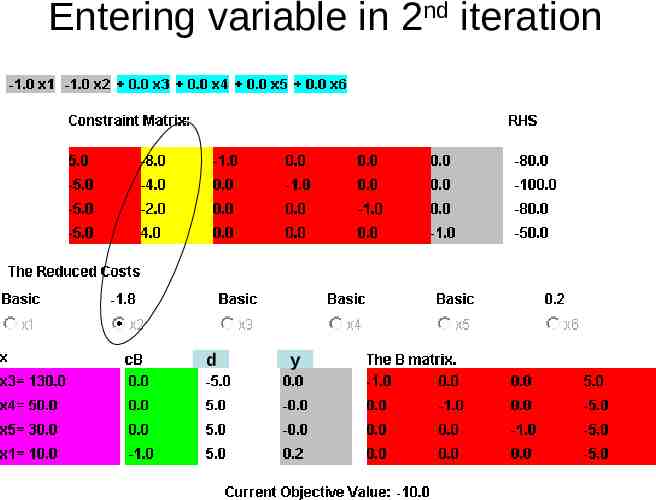
New cost cx ' cB xB' c N x N' cB ( xB B 1 Nx N' ) c N x N' ' ' ' 1 ' cx cB xB c N x N cB xB (c N cB B N ) x N Change in cost ' 1 ' cx cx (c N cB B N ) x N The term in bracket is called reduced cost 1 c c N cB B N If all elements of it are non-negative, it is already optimal Otherwise choose the non-basic variable corresponding to most negative value to enter the basic

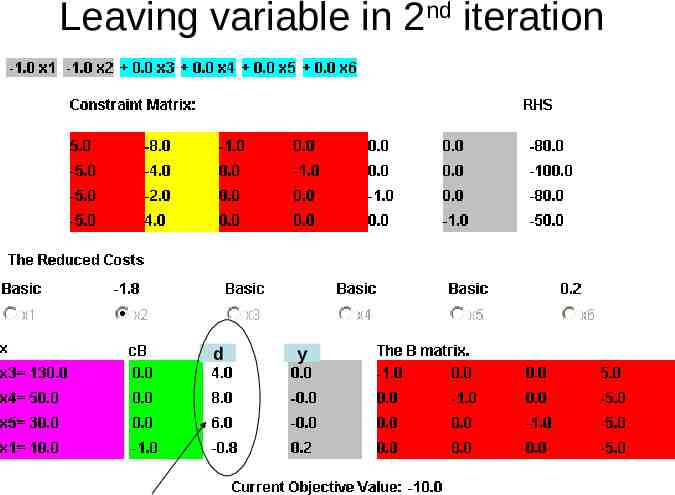
How to find out outgoing basic variable? xB' B 1 Nx N' B 1b 1 Let d be the column of B N that mutilpies with new basic variable xi . It can be increased until one (say k th ) component of xB' becomes 0. Min value of 1 kth component of B b( xB ) kth component of d

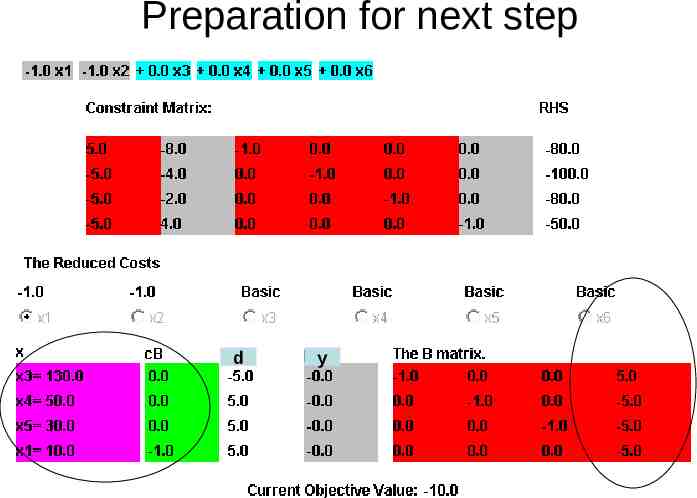
Few steps of simplex algorithm 1 Compute reduced cost c N cB B N If all 0, optimal stop. Otherwise choose the most negative component Corresponding variable enters basis Compute the ratios for finding out leaving basis Update basic variables and B for next step ' B 1 x xB B Nx ' N

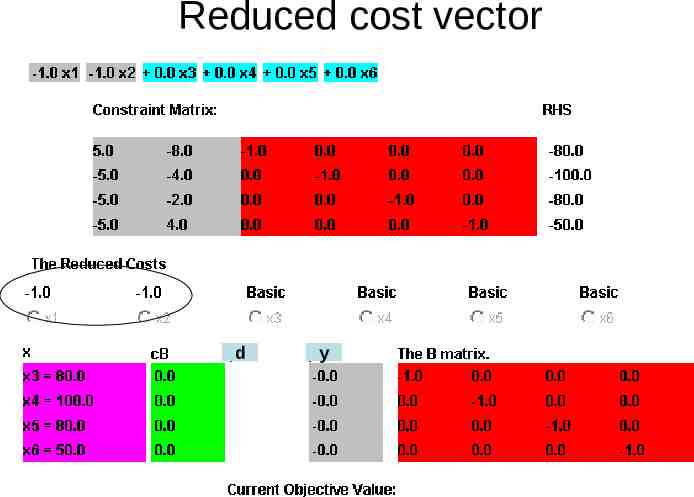
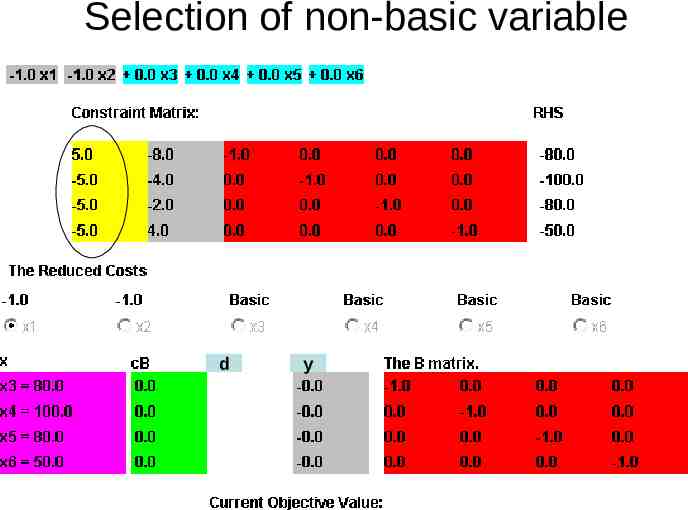
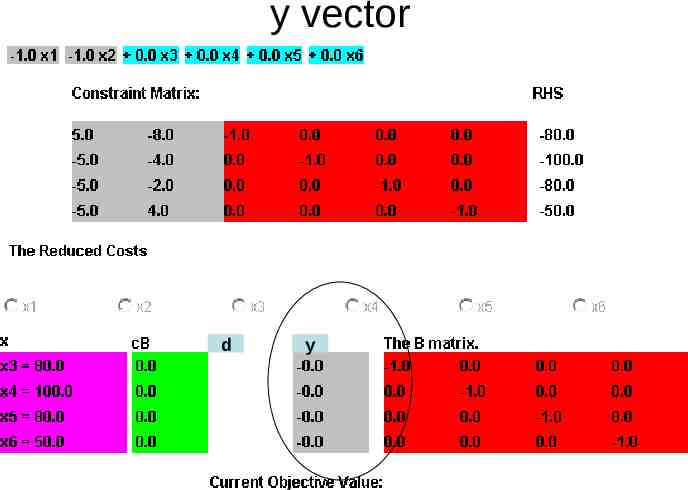
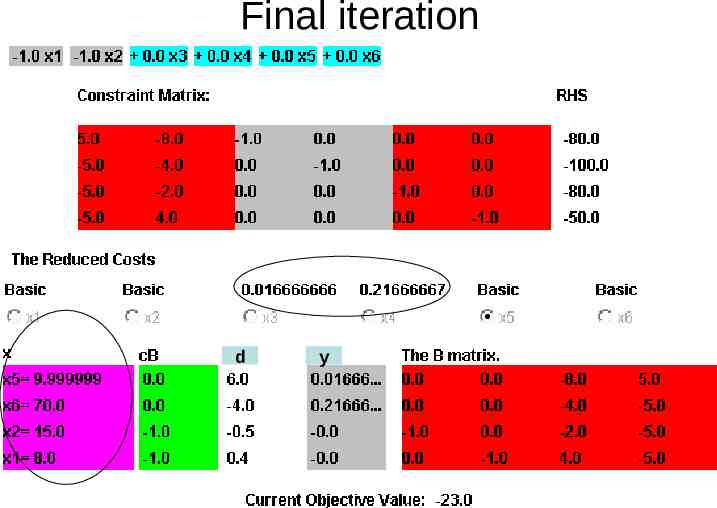
Smart way of doing BxB b gives xB yB cB gives y and reduced cost c N yN Bd a where a is the column of N , gives d xB gives info about leaving variable d

Start d y

Reduced cost vector d y

Selection of non-basic variable d y

y vector d y

Selection of leaving basic variable d y

Preparation for next step d y

Entering variable in 2nd iteration d y

Leaving variable in 2nd iteration d y

Preparation for 3rd iteration d y

Final iteration d y

Done so far Basics of (revised) Simplex algorithm – Formulation – Corners, basic variables, non-basic variables – How to move from corner to corners – Optimal value

Agenda Introduction Basics of Simplex algorithm Formulations for the CSP (Delayed) Column Generation Branch-and-price Flow formulation of CSP & solution Conclusions

First step to solution - Formulation Min s.t. : K y k k 1 K x ik bi k 1 m w x i ik Wy k i 1 i 1, , m k 1, , K yk 0 or 1 xik 0 and integer k 1, , K K k no. of available raws index for a raw m i yk 1 if k th raw is used, 0 otherwise no. of finals of i th width cut from k th raw xik k 1, , K i 1, , m no. of different widths index for a width Kantorovich formulation

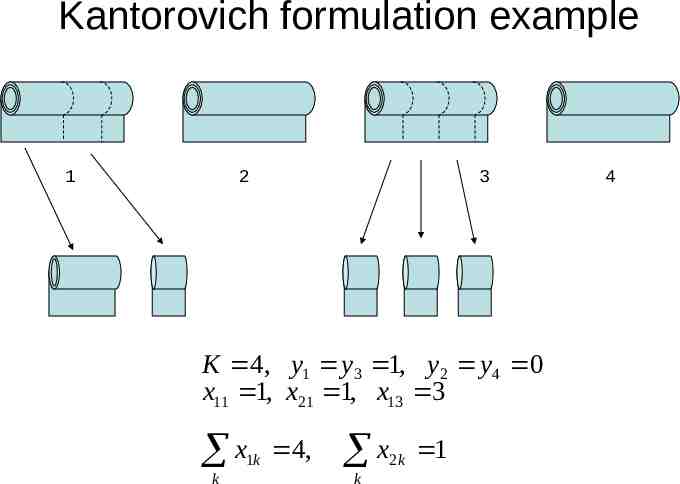
Kantorovich formulation example 1 2 3 K 4, y1 y3 1, y2 y4 0 x11 1, x21 1, x13 3 x 1k k 4, x k 2k 1 4

LP relaxation Integer programming is hard Convert it to a linear program Min K y k k 1 K s.t. : x ik bi k 1 m wx i ik Wy k i 1 i 1, , m k 1, , K 0 yk 1 yk 0 or 1 xik 0 and integer k 1, , K k 1, , K i 1, , m K k no. of available raws index for a raw m i no. of different widths index for a width yk 1 if k th raw is used, 0 otherwise no. of finals of i th width cut from k th raw xik

LP relaxation (2) LP relaxation is poor For our example, optimal LP objective is 120.5 The optimal integer objective solution value is 157 Gap is 36.5 It can be as bad as ½ of the integer solution Can we get a better LP relaxation?

Another Formulation Min x a j j J s.t. : ij x j bi i 1, , m j J x j 0 and integer j J i index for a width m no. of different widths j a cutting pattern J xj set of all possible patterns no. of raws cut in pattern j no. of finals of i th width cut from pattern j aij Gilmore-Gomory Formulation

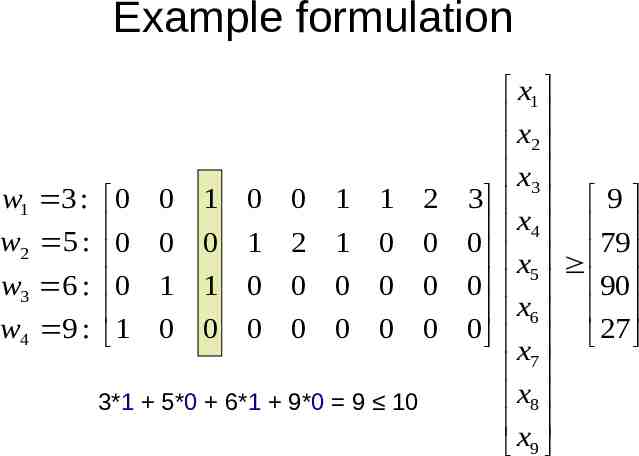
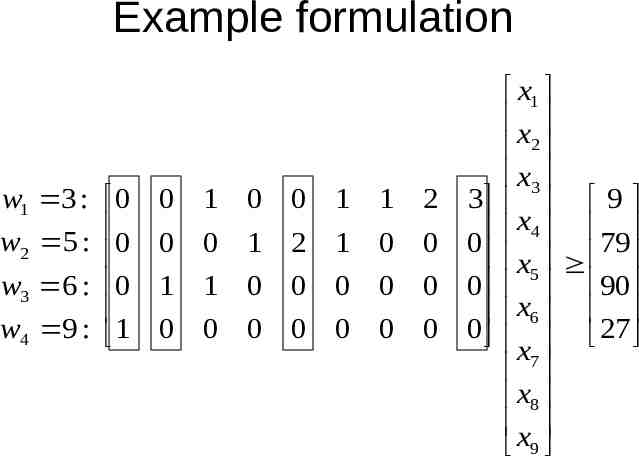
Example formulation w1 3 : 0 w2 5 : 0 w3 6 : 0 w4 9 : 1 0 1 0 0 1 1 2 3 0 0 1 2 1 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 3*1 5*0 6*1 9*0 9 10 x1 x 2 x3 9 x4 79 x5 90 x6 x 27 7 x8 x 9

LP relaxation of Gilmore-Gomory LP relaxation is better For our example, 156.7 Integer objective solution, 157 Gap is 0.3 Conjecture: Gap is less than 2 for practical cutting stock problems

Issues The number of columns are exponential Optimal value is still not integer Gilmore-Gomory proposed an ingenuous way of working with less columns Branch-and-price to solve the other problem

Done so far Basics of (revised) Simplex algorithm – Formulation – Corners, basic variables, non-basic variables – How to move from corner to corners – Optimal value Formulation of the CSP – LP relaxation – Bounds

Agenda Introduction Basics of Simplex algorithm Formulations for the CSP (Delayed) Column Generation Branch-and-price Flow formulation of CSP & solution Conclusions

Column Generation In pricing step of simplex algorithm one basic variable leaves and one non-basic variable enters the basis This decision is made from the reduced cost vector c N cB B 1 N or c N yN The component with most negative value determines the entering variable

Column Generation (2) In terms of columns, we need to find arg min{c j ya j a j is a column of N } j That is equivalent to finding a such that min{c(a ) ya a is a column of A} For cutting stock problem, cj 1, hence it is equivalent to max{ ya ya 1} With implicit constraint wa W Pricing sub-problem

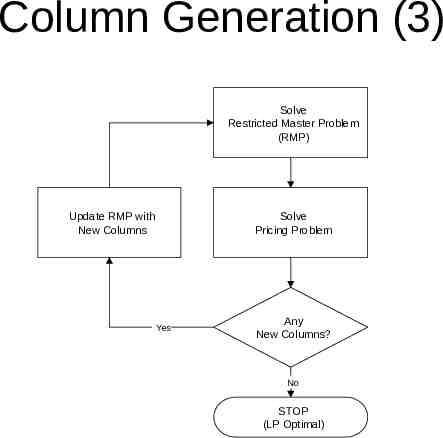
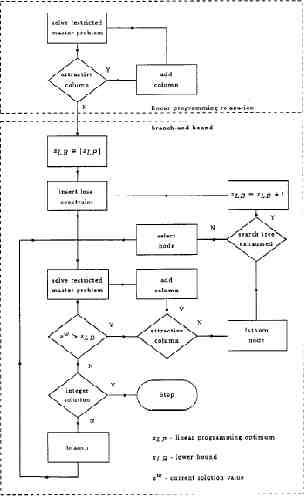
Column Generation (3) Solve Restricted Master Problem (RMP) Update RMP with New Columns Solve Pricing Problem Yes Any New Columns? No STOP (LP Optimal)

Example formulation w1 3 : 0 w2 5 : 0 w3 6 : 0 w4 9 : 1 0 1 0 0 1 1 2 3 0 0 1 2 1 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 x1 x 2 x3 9 x4 79 x5 90 x6 x 27 7 x8 x 9

9 3 79 0 C B , B 90 0 27 0 0 0 0 9/3 3 79 / 2 39.5 2 0 0 , x B 90 / 1 90 0 1 0 0 0 1 27 / 1 27 yB 1 1 1 1 y 1 / 3 1 / 2 1 1 1 1 we need to maximize a1 a2 1.a3 1.a4 1 3 2 Given knapsack constraint 3a1 5a2 6a3 9a4 10 Using enumeration or dynamic programming, we can find T a 1 0 1 0

1 Bd a d 0 1 0 3 T T 1 T x B / d 3 / * 90 / 1 * 9 * 90 * 3 t 9, first column in B is replaced 1 0 B 1 0 0 0 0 t 9 9 39.5 39.5 39.5 2 0 0 , x B 90 t.d 3 90 9.1 81 0 1 0 0 0 1 27 27 27

1 0 B 1 0 0 0 0 9 2 0 0 39.5 , xB 81 0 1 0 0 0 1 27 yB 1 1 1 1 y 0 1 / 2 1 1 1 we need to maximize 0.a1 a2 1.a3 1.a4 1 2 Given knapsack costraint 3a1 5a2 6a3 9a4 10 We can not get solution of subproblem 1 Hence xB is already optimal Solution 9 39.5 81 27 156.5

Done so far Basics of (revised) Simplex algorithm – – – – Formulation Corners, basic variables, non-basic variables How to move from corner to corners Optimal value Formulation of the CSP – LP relaxation – Bounds Delayed column generation – Restricted master problem – Sub-problem to generate column – Repeated till optimal

Agenda Introduction Basics of Simplex algorithm Formulations for the CSP (Delayed) Column Generation Branch-and-price Flow formulation of CSP & solution Conclusions

Integer solution A formulation of the problem which gives ‘good’ LP relaxation Solved the LP relaxation using column generation But, the LP relaxation is not the ultimate goal, we need integer solution In the example x2 is 39.5 One way is to rounding

What to do if there are multiple fractional variables? The method commonly followed is branch and-bound technique of solving integer programs Basic fundae – create multiple sub-problems with extra constraints – solve the sub-problems using column generation – take the best of solutions to the sub problems

Key is the rules of dividing into sub problems (this is called branching strategy) Things to look into – Branching rule does not destroy column generation sub problem property – Efficiency of the process Ingenuity of the formulation and branching strategy Use of running bounds to prune (fathomed) This technique is called branch-and-price We see another formulation next

Done so far Basics of (revised) Simplex algorithm – – – – Formulation Corners, basic variables, non-basic variables How to move from corner to corners Optimal value Formulation of the CSP – LP relaxation – Bounds Delayed column generation – Restricted master problem – Sub-problem to generate column – Repeated till optimal Branch-and-price – Basic fundae

Agenda Introduction Basics of Simplex algorithm Formulations for the CSP (Delayed) Column Generation Branch-and-price Flow formulation of CSP & solution Conclusions

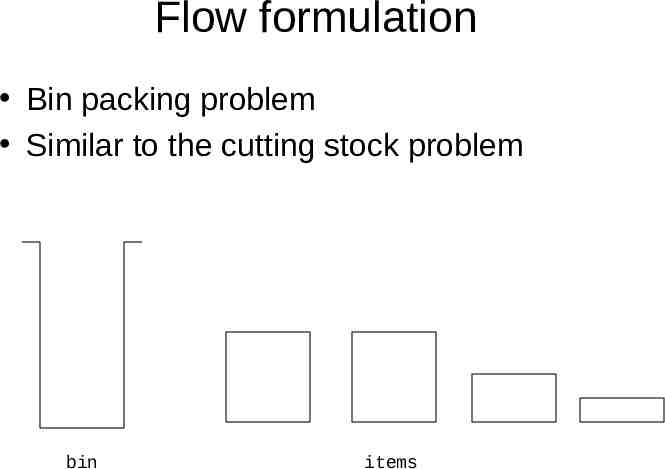
Flow formulation Bin packing problem Similar to the cutting stock problem bin items

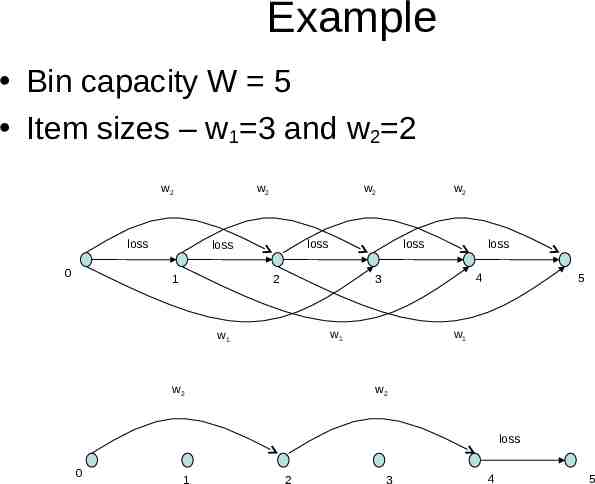
Example Bin capacity W 5 Item sizes – w1 3 and w2 2 w2 w2 loss 0 w2 loss loss 1 w2 loss 2 loss 4 3 w1 w1 w2 5 w1 w2 loss 0 1 2 3 4 5

Formulation equations Problem is equivalent to finding minimum flow between nodes 0 & W Min z s.t. : j 0 z , xij x jk 0, i 1,2, ,W 1 ij A jk A z, j W xk (k wd ) bd d 1,2, , m k ( k wd ) A xij integer 0 z integer 0

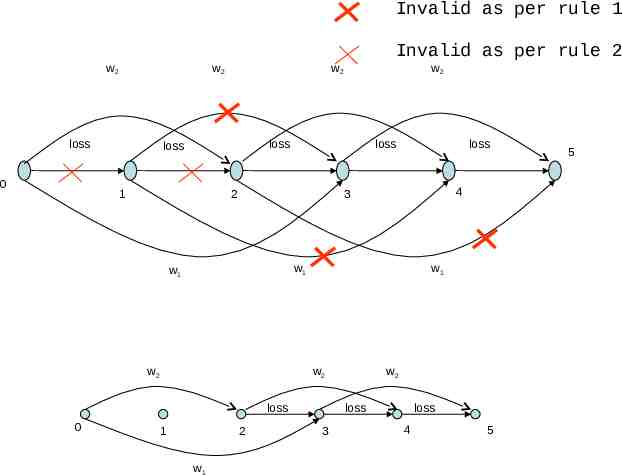
Issue of symmetry in the graph 3 rules to reduce symmetry 1. Arcs are specified according to decreasing width 2. A bin can never start with a loss 3. Number of consecutive arcs corresponding to a single item size must not exceed number of orders

Invalid as per rule 1 w2 w2 loss 0 w2 w2 loss loss 1 loss 2 loss 4 3 w1 w1 w2 w1 w2 loss 0 Invalid as per rule 2 1 2 w1 w2 loss 3 loss 4 5 5

Branch-and-price The sub-problem finds an longest unit flow path where cost of each arc is given by y vector Branching heuristics – Xij ceil(xij) – Xij floor(xij)

Few other points Loss constraints from the LP relaxation value is equated with the sum of loss variables With the above constraint it can be shown that the solution will be always integral The algorithm uses this fact by incrementally adding the lower bound This is done finite no. of times No of new constraints are added is finite Algorithm runs in pseudo-polynomial time

Conclusions & Future work Column generation is a success story in large scale integer programming The flexibility to work with a few columns make real life problems tractable Ingenuous formulations and branching heuristics are used to improve efficiency Need to explore more applications with different heuristics

Acknowledgements Valerio de Carvalho for borrowing some of his explanations exactly http://www-fp.mcs.anl.gov/otc/Guide/Ca seStudies/simplex/applet/SimplexTool.h tml for the java applet AMPL & CPLEX tools My guide

Thank you!