Cliquez sur l’icône pour ajouter une image SCALABLE NETWORK

Cliquez sur l'icône pour ajouter une image SCALABLE NETWORK EMBEDDING LOUVAINNE: HIERARCHICAL LOUVAIN METHOD FOR HIGH QUALITY AND SCALABLE NETWORK EMBEDDING Ayan Kumar Bhowmick1, Koushik Meneni1, Maximilien Danisch2, Jean-Loup Guillaume3, and Bivas Mitra1 1. Department of CSE, Indian Institute of Technology, Kharagpur 2. Sorbonne Université, CNRS, LIP6, Paris, France

NETWORK DATA IS UBIQUITOUS Social networks DYNAMICS ON AND OF COMPLEX NETWORKS 2020 Biology networks Information 2 18/09/2020 2

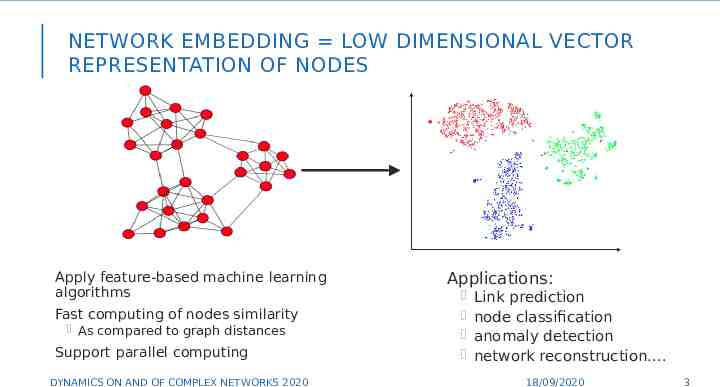
NETWORK EMBEDDING LOW DIMENSIONAL VECTOR REPRESENTATION OF NODES Apply feature-based machine learning algorithms Fast computing of nodes similarity As compared to graph distances Support parallel computing DYNAMICS ON AND OF COMPLEX NETWORKS 2020 Applications: Link prediction node classification anomaly detection network reconstruction. 3 18/09/2020 3

CHALLENGE: BILLION-SCALE NETWORK DATA Social networks WeChat: 1 billion monthly active users Facebook: 2 billion active users E-commerce networks Amazon: 353 million products, 310 million users, billion orders/year Citation networks Aminer: 130 million authors, 233 million publications, 754 million citations Challenge: design a (really) scalable network embedding method DYNAMICS ON AND OF COMPLEX NETWORKS 2020 18/09/2020 4 4

EXISTING LITERATURE Domain Random walk based approaches Perozzi et al. (KDD’14), Yang et al. (IJCAI’15), Grover et al. (KDD’16), Pan et al. (IJCAI’16), Ribeiro et al. (KDD’17), Zhang et al. (ICDM’18) Matrix factorization based approaches Cao et al. (CIKM’15), Ou et al. (KDD’16), Wang et al. (AAAI’17), Huang et al. (WSDM’17), Qiu et al. (WWW’19), Zhang et al. (IJCAI’19) Deep learning based approaches Cao et al. (AAAI’16), Wang et al. (KDD’16) Edge modeling approaches Tang et al. (WWW’15), Wang et al. (CIKM’16), Wang et al. (AAAI’18) Hybrid approaches Yang et al. (ICML’16), Chen et al. (AAAI’18), Zhu et al. (WWW’19) Hierarchical Chen et al. (AAAI’18), Ma et al. (KDD’18), Liang et al. approaches (arXiv) DYNAMICS ON AND OF COMPLEX NETWORKS 2020 18/09/2020 5 5

LIMITATIONS OF EXISTING LITERATURE ProNE (IJCAI’19) – sparse matrix factorization “we can project that it costs ProNE only 29 hours to embed a network of 0.1 billion nodes and 0.5 billion edges by using one thread, while it takes LINE over one week and may take DeepWalk/node2vec several months by using 20 threads” High quality embedding but limited scaling RandNE (ICDM’18) - iterative Gaussian random projection approach “RandNE can boost the efficiency by more than 24 times over the baselines on all networks” Very fast but quality can be compromised in some cases. Original code in matlab (and a more recent version in python), we redeveloped it in C Our goal: propose a network embedding method that: Scales well for billion-scale graphs, even more than randNE Preserves embedding quality for billion-scale graphs 6 DYNAMICS ON AND OF COMPLEX NETWORKS 2020 18/09/2020 6

PROBLEM STATEMENT Develop LouvainNE, a fast and highly scalable network embedding framework Use the notion of a hierarchy of communities LouvainNE Large-scale network DYNAMICS ON AND OF COMPLEX NETWORKS 2020 Low-dimensional embedding vectors 7 18/09/2020 7

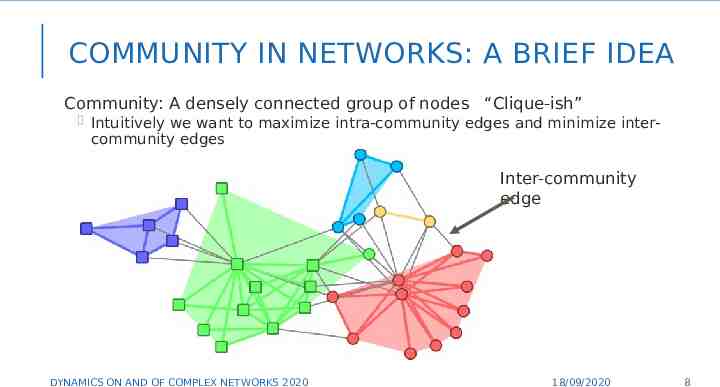
COMMUNITY IN NETWORKS: A BRIEF IDEA Community: A densely connected group of nodes “Clique-ish” Intuitively we want to maximize intra-community edges and minimize intercommunity edges Inter-community edge 8 DYNAMICS ON AND OF COMPLEX NETWORKS 2020 18/09/2020 8

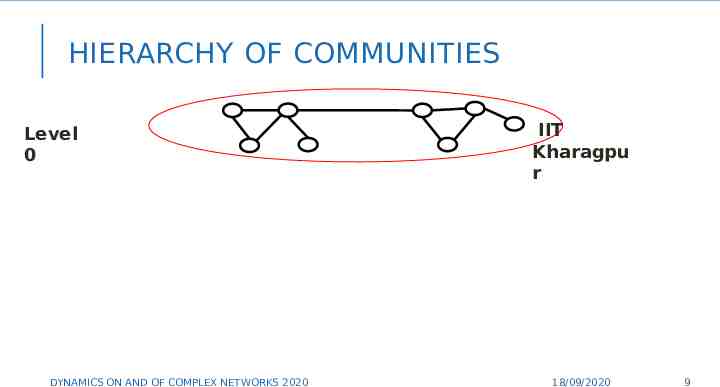
HIERARCHY OF COMMUNITIES Level 0 IIT Kharagpu r 9 DYNAMICS ON AND OF COMPLEX NETWORKS 2020 18/09/2020 9

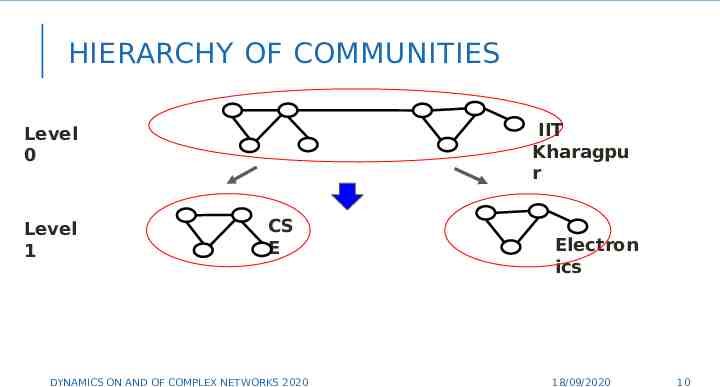
HIERARCHY OF COMMUNITIES IIT Kharagpu r Level 0 Level 1 CS E Electron ics 10 DYNAMICS ON AND OF COMPLEX NETWORKS 2020 18/09/2020 10

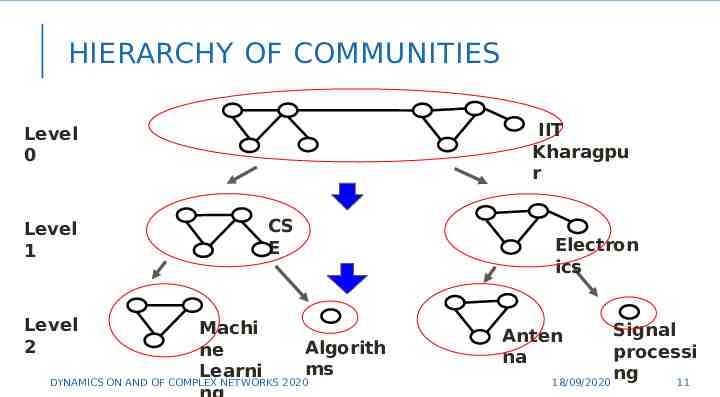
HIERARCHY OF COMMUNITIES IIT Kharagpu r Level 0 Level 1 Level 2 CS E Machi Algorith ne ms Learni DYNAMICS ON AND OF COMPLEX NETWORKS 2020 Electron ics Signal processi 11 ng 18/09/2020 11 Anten na

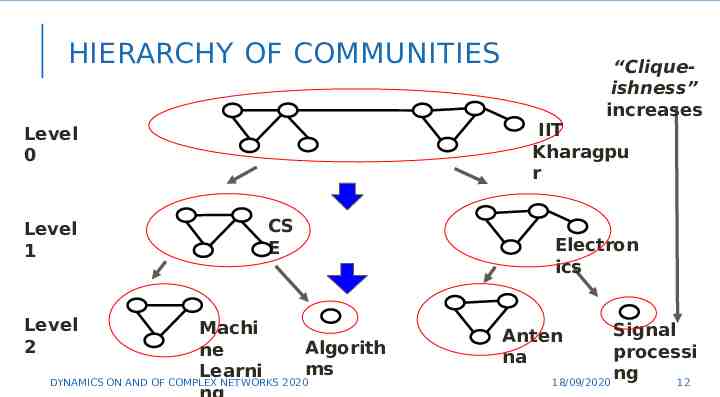
HIERARCHY OF COMMUNITIES IIT Kharagpu r Level 0 Level 1 Level 2 “Cliqueishness” increases CS E Machi Algorith ne ms Learni DYNAMICS ON AND OF COMPLEX NETWORKS 2020 Electron ics Signal processi 12 ng 18/09/2020 12 Anten na

COMMUNITY DETECTION: A BRIEF IDEA A research subject with work for more than 20 years Hundreds of solutions [Fortunato’10, Fortunato’16] To have a fast embedding, it is necessary to have a fast and efficient community detection method Label Propagation [Raghavan’07] Louvain [Blondel’08] Infomap [Rosvall’08] Leiden [Traag’19] Many other solutions could be used but scaling would no longer be possible Santo Fortunato. Community detection in graphs. Physics Reports 486 (3–5), 2010, Pages 75-174. Santo Fortunato, Darko Hric. Community detection in networks: A user aguide. Physics Reports 659, 2016, Pages 1-44. Nandini Raghavan, Réka Albert, Soundar Kumara. Near Linear Time Algorithm to Detect Community Structures in Large-Scale Networks. Physical Review E 76:036106, 2007. Vincent D Blondel, Jean-Loup Guillaume, Renaud Lambiotte and Etienne Lefebvre. Fast unfolding of communities in large networks. Journal of Statistical Mechanics: Theory and Experiment, Volume 2008, October 2008 Martin Rosvall and Carl T. Bergstrom. Maps of information flow reveal community structure in complex networks. PNAS 105, 1118 (2008) Traag, V.A., Waltman, L. & van Eck, N.J. From Louvain to Leiden: guaranteeing well-connected communities. Sci Rep 9, 5233 (2019). 13 DYNAMICS ON AND OF COMPLEX NETWORKS 2020 18/09/2020 13

WHY LOUVAIN? Good partitions (in terms of quality) Listed among the top algorithms in terms of quality of the solutions and the results achieved on benchmarks Very fast Only Leiden might be faster Strong expertise Developping the LouvainNE solution required a complete redevelopment of Louvain https://github.com/jlguillaume/louvain https://github.com/maxdan94/LouvainNE 14 DYNAMICS ON AND OF COMPLEX NETWORKS 2020 18/09/2020 14

OUR APPROACH TO THE SOLUTION Rely on the “hierarchy” of communities in a network for Scalable Network Embedding Identify communities using Louvain Time complexity “O(m)” 15 DYNAMICS ON AND OF COMPLEX NETWORKS 2020 18/09/2020 15

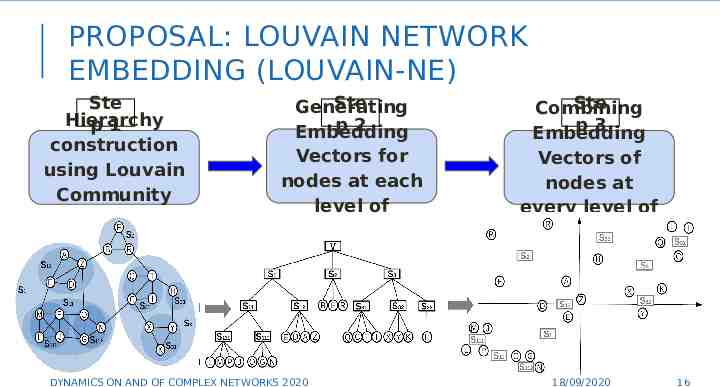
PROPOSAL: LOUVAIN NETWORK EMBEDDING (LOUVAIN-NE) Ste Hierarchy p1 construction using Louvain Community Detection Ste Generating p2 Embedding Vectors for nodes at each level of hierarchy Ste Combining p3 Embedding Vectors of nodes at every level of hierarchy 16 DYNAMICS ON AND OF COMPLEX NETWORKS 2020 18/09/2020 16

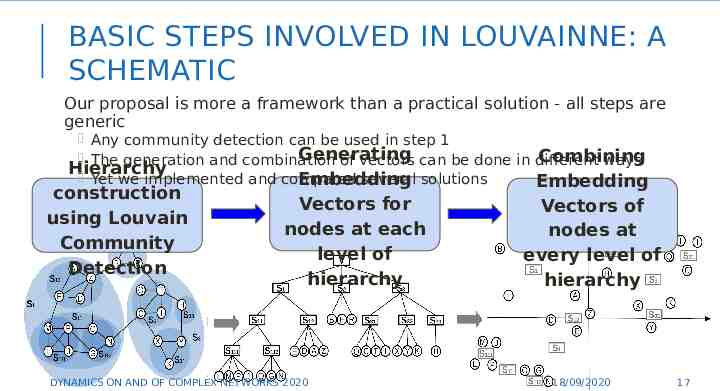
BASIC STEPS INVOLVED IN LOUVAINNE: A SCHEMATIC Our proposal is more a framework than a practical solution - all steps are generic Any community detection can be used in step 1 Generating Combining The generation and combination of vectors can be done in different ways Hierarchy Yet we implemented and compared several solutions Embedding Embedding construction using Louvain Community Detection Vectors for nodes at each level of hierarchy Vectors of nodes at every level of hierarchy 17 DYNAMICS ON AND OF COMPLEX NETWORKS 2020 18/09/2020 17

STEP 1 Hierarchical Clustering using Louvain 18 DYNAMICS ON AND OF COMPLEX NETWORKS 2020 18/09/2020 18

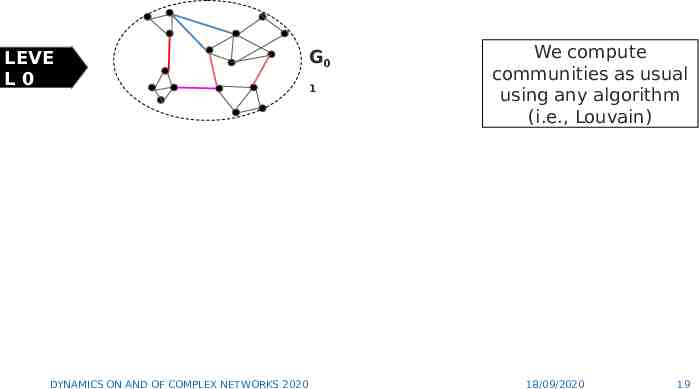
LEVE L0 DYNAMICS ON AND OF COMPLEX NETWORKS 2020 G0 1 We compute communities as usual using any algorithm (i.e., Louvain) 18/09/2020 19

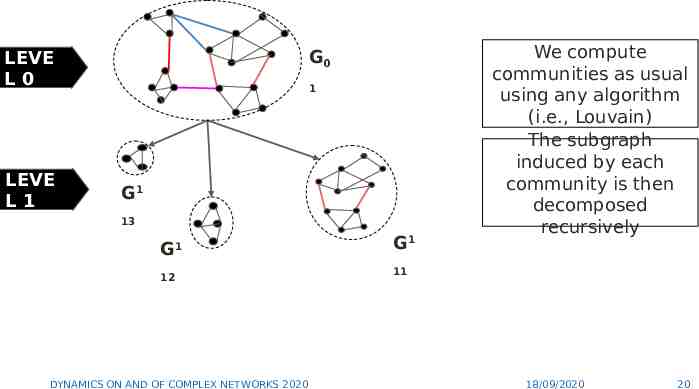
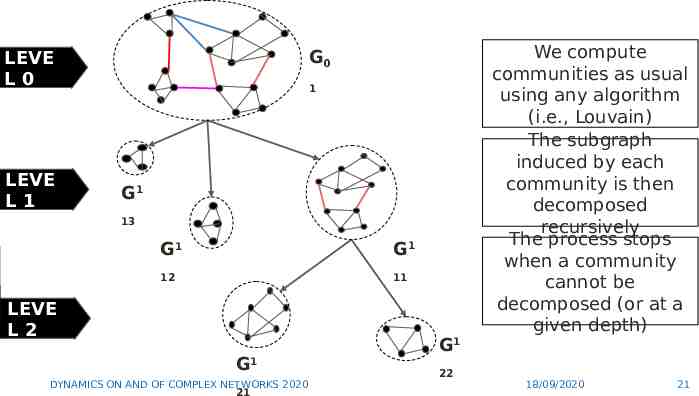
G0 LEVE L0 LEVE L1 1 G1 13 G1 12 DYNAMICS ON AND OF COMPLEX NETWORKS 2020 G1 We compute communities as usual using any algorithm (i.e., Louvain) The subgraph induced by each community is then decomposed recursively 11 18/09/2020 20

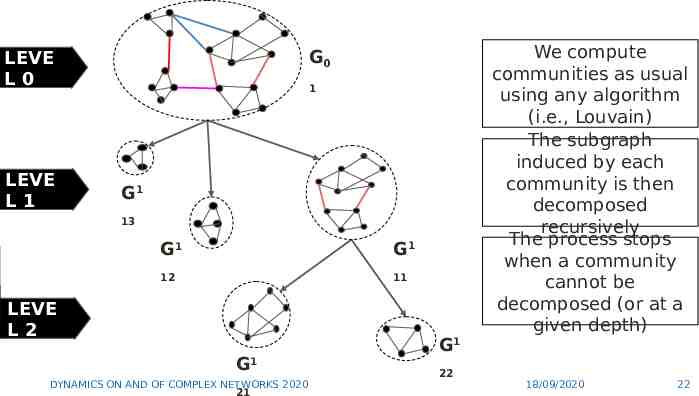
G0 LEVE L0 LEVE L1 1 G1 13 G1 G1 12 11 LEVE L2 G1 DYNAMICS ON AND OF COMPLEX NETWORKS 2020 21 G1 22 We compute communities as usual using any algorithm (i.e., Louvain) The subgraph induced by each community is then decomposed recursively The process stops when a community cannot be decomposed (or at a given depth) 18/09/2020 21

G0 LEVE L0 LEVE L1 1 G1 13 G1 G1 12 11 LEVE L2 G1 DYNAMICS ON AND OF COMPLEX NETWORKS 2020 21 G1 22 We compute communities as usual using any algorithm (i.e., Louvain) The subgraph induced by each community is then decomposed recursively The process stops when a community cannot be decomposed (or at a given depth) 18/09/2020 22

STEP 2 Generating Node Embeddings at Each Level (Stochastic Embedding) Ignoring the inter-community edges 23 DYNAMICS ON AND OF COMPLEX NETWORKS 2020 18/09/2020 23

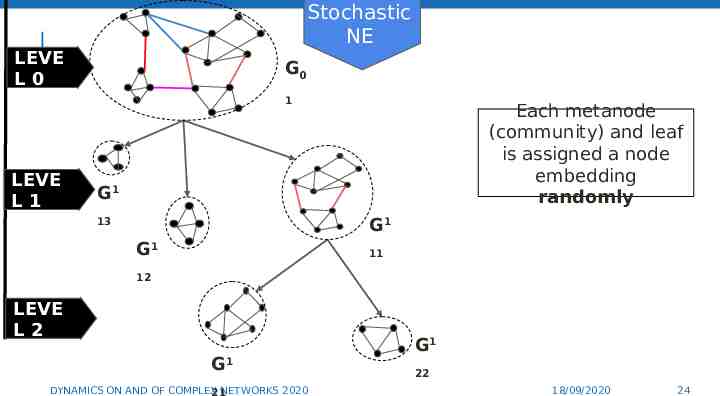
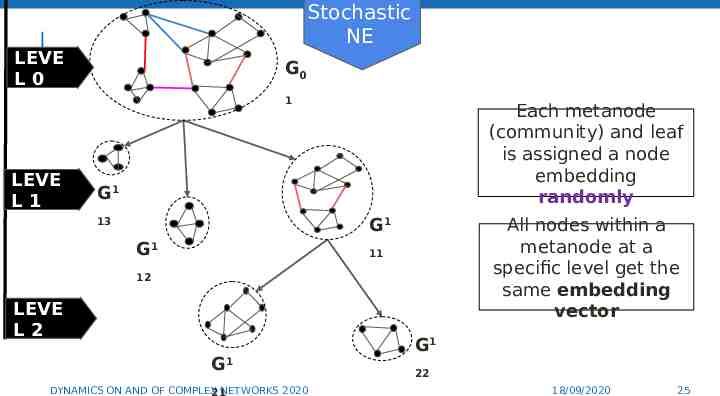
Stochastic NE LEVE L0 G0 1 LEVE L1 Each metanode (community) and leaf is assigned a node embedding randomly G1 G1 13 G1 11 12 LEVE L2 G1 DYNAMICS ON AND OF COMPLEX NETWORKS 2020 21 G1 24 22 18/09/2020 24

Stochastic NE LEVE L0 G0 1 LEVE L1 Each metanode (community) and leaf is assigned a node embedding randomly G1 G1 13 G1 All nodes within a metanode at a specific level get the same embedding vector 11 12 LEVE L2 G1 DYNAMICS ON AND OF COMPLEX NETWORKS 2020 21 G1 25 22 18/09/2020 25

STEP 2 - SMARTER VARIANT Generating Node Embeddings at Each Level (Standard Embedding) Ignoring the inter-community edges 26 DYNAMICS ON AND OF COMPLEX NETWORKS 2020 18/09/2020 26

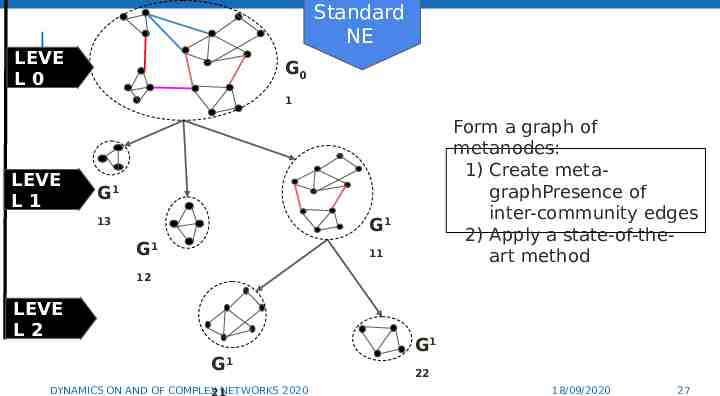
Standard NE LEVE L0 G0 1 LEVE L1 Form a graph of metanodes: 1) Create metagraphPresence of inter-community edges 2) Apply a state-of-theart method G1 G1 13 G1 11 12 LEVE L2 G1 DYNAMICS ON AND OF COMPLEX NETWORKS 2020 21 G1 27 22 18/09/2020 27

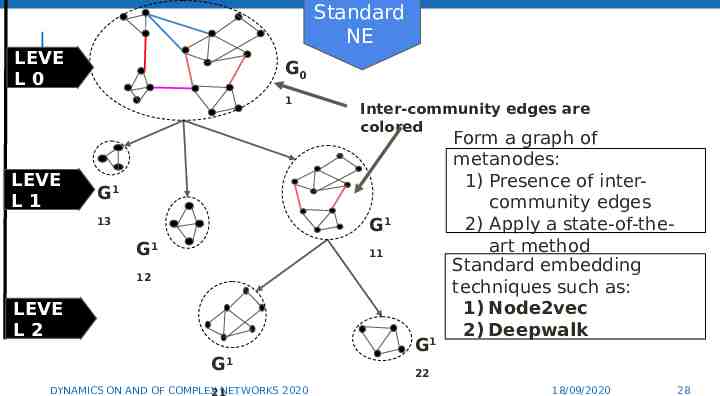
Standard NE LEVE L0 G0 1 LEVE L1 Inter-community edges are colored G1 G1 13 G1 11 12 LEVE L2 G1 DYNAMICS ON AND OF COMPLEX NETWORKS 2020 21 G1 Form a graph of metanodes: 1) Presence of intercommunity edges 2) Apply a state-of-theart method Standard embedding techniques such as: 1) Node2vec 2) Deepwalk 28 22 18/09/2020 28

STEP 3 Combining Node Embeddings Generated at Different Levels 29 DYNAMICS ON AND OF COMPLEX NETWORKS 2020 18/09/2020 29

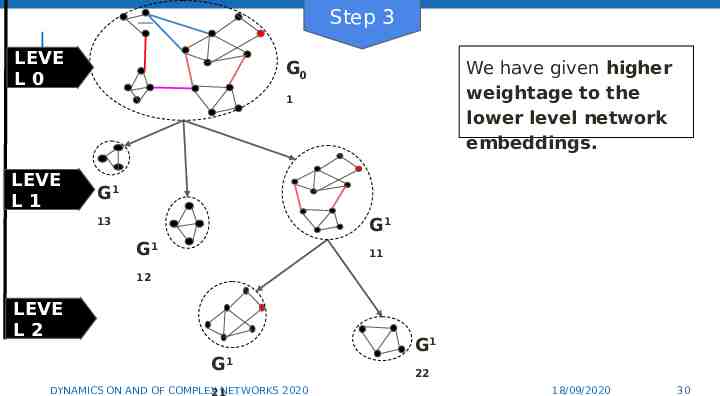
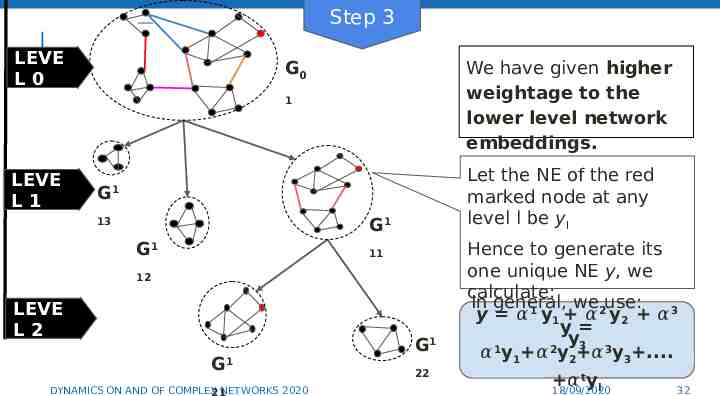
Step 3 LEVE L0 G0 We have given higher weightage to the lower level network embeddings. 1 LEVE L1 G1 G1 13 G1 11 12 LEVE L2 G1 DYNAMICS ON AND OF COMPLEX NETWORKS 2020 21 G1 30 22 18/09/2020 30

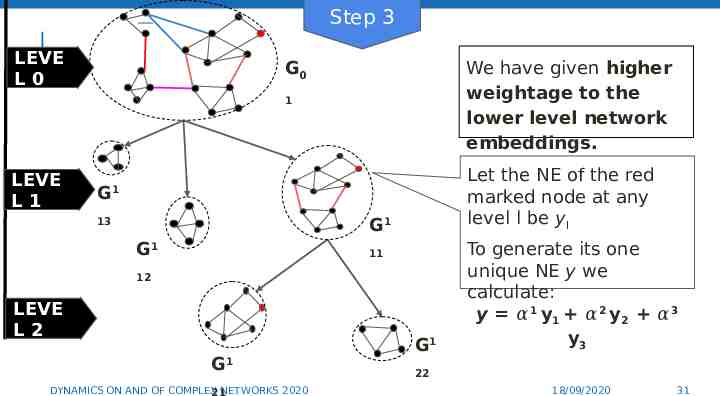
Step 3 LEVE L0 We have given higher weightage to the lower level network embeddings. G0 1 LEVE L1 Let the NE of the red marked node at any level l be yl G 1 G1 13 G1 11 12 LEVE L2 G1 DYNAMICS ON AND OF COMPLEX NETWORKS 2020 21 G1 To generate its one unique NE y we calculate: y 𝛼1 y1 𝛼2 y2 𝛼3 y3 31 22 18/09/2020 31

Step 3 LEVE L0 We have given higher weightage to the lower level network embeddings. G0 1 LEVE L1 Let the NE of the red marked node at any level l be yl G 1 G1 13 G1 11 12 LEVE L2 G1 DYNAMICS ON AND OF COMPLEX NETWORKS 2020 21 G1 22 Hence to generate its one unique NE y, we calculate: In general, we use: y 𝛼1 y1 𝛼2 y2 𝛼3 y y3 𝛼1y1 𝛼2y2 𝛼3y3 . 𝛼tyl 18/09/2020 32 32

TIME COMPLEXITY OF LOUVAINNE Time taken for different steps: Hierarchy construction step: O(Louvain(G) x h) where h is height of the hierarchy tree LG We assume that Louvain on a given graph takes no less time that Louvain on the set of induced subgraphs Step 2 (level specific embedding) and Step 3 (combining) together takes: O(d.N) If Louvain has a linear complexity O(M) then Overall time complexity : O(M.h d.N) 33 DYNAMICS ON AND OF COMPLEX NETWORKS 2020 18/09/2020 33

Cliquez sur l'icône pour ajouter une image EVALUATION 34

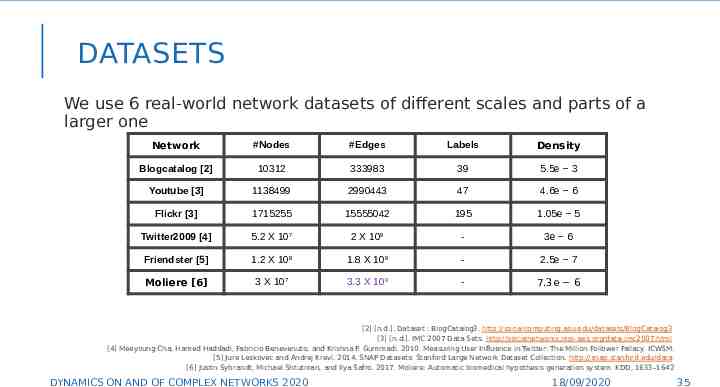
DATASETS We use 6 real-world network datasets of different scales and parts of a larger one Network #Nodes #Edges Labels Density Blogcatalog [2] 10312 333983 39 5.5e 3 Youtube [3] 1138499 2990443 47 4.6e 6 Flickr [3] 1715255 15555042 195 1.05e 5 Twitter2009 [4] 5.2 X 107 2 X 109 - 3e 6 Friendster [5] 1.2 X 108 1.8 X 109 - 2.5e 7 Moliere [6] 3 X 107 3.3 X 109 - 7.3e 6 [2] [n.d.]. Dataset : BlogCatalog3. http://socialcomputing.asu.edu/datasets/BlogCatalog3 [3] [n.d.]. IMC 2007 Data Sets. http://socialnetworks.mpi-sws.org/data-imc2007.html [4] Meeyoung Cha, Hamed Haddadi, Fabricio Benevenuto, and Krishna P. Gummadi. 2010. Measuring User Influence in Twitter: The Million Follower Fallacy. ICWSM. [5] Jure Leskovec and Andrej Krevl. 2014. SNAP Datasets: Stanford Large Network Dataset Collection. http://snap.stanford.edu/data [6] Justin Sybrandt, Michael Shtutman, and Ilya Safro. 2017. Moliere: Automatic biomedical hypothesis generation system. KDD, 1633–1642 35 DYNAMICS ON AND OF COMPLEX NETWORKS 2020 18/09/2020 35

BASELINE ALGORITHMS HARP: Meta-strategy [7] for embedding graphs preserving higher-order structural features and employs a hierarchical embedding approach MILE: Developed a framework [8] similar to [7] where it scales up the performance of a standard embedding method even for large graphs using hybrid graph matching RandNE: Gaussian random projection based approach [10] to learn embeddings, while preserving the higher-order proximities using an iterative projection procedure NetSMF: Leverages spectral graph sparsification technique [11] to construct a matrix with significantly fewer non-zero entries to learn high quality node embeddings in a graph [7] Haochen Chen, Bryan Perozzi, Yifan Hu, and Steven Skiena. 2018. Harp: Hierarchical representation learning for networks. AAAI, 2127–2134 ProNE: Fast and network embedding framework [9],Embedding. thatarXiv leverages [8] Jiongqian Liang, scalable Saket Gurukar, and Srinivasan Parthasarathy. 2018. MILE: A Multi-Level Framework for Scalable Graph preprint (2018) [9] Jie Zhang, Yuxiao Dong, Yan Wang, Jie Tang, and Ming Ding. 2019. ProNE: Fast and Scalable Network Representation Learning. IJCAI, 4278-4284 on spectral propagation toWang, enhance quality embeddings [10] Ziwei Zhang, Peng Cui, Haoyang Li, Xiao and Wenwu Zhu. the 2018. Billion-scale Networkof Embedding with Iterative Random Projection. ICDM, 787–796 36 [11] Jiezhong Qiu, Yuxiao Dong, Hao Ma, Jian Li, Chi Wang, Kuansan Wang, and Jie Tang. 2019. Netsmf: Large-scale network embedding as sparse matrix factorization. WWW, 1509–1520 DYNAMICS ON AND OF COMPLEX NETWORKS 2020 18/09/2020 36

EXPERIMENTAL EVALUATION We evaluate the performance of LouvainNE against the state-of-the-art in 2 ways Scalabity Quality Scalability Compare the time taken to obtain embeddings on multiple datasets Most embedding techniques do not really scale Evaluation on downstream tasks - Validate the embedding quality Network reconstruction Multi-label classification DYNAMICS ON AND OF COMPLEX NETWORKS 2020 37 18/09/2020 37

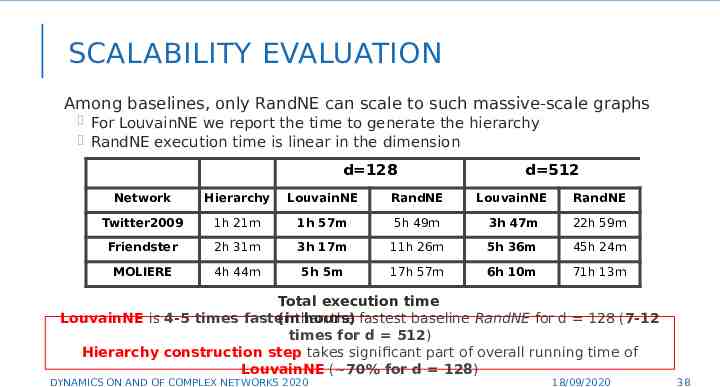
SCALABILITY EVALUATION Among baselines, only RandNE can scale to such massive-scale graphs For LouvainNE we report the time to generate the hierarchy RandNE execution time is linear in the dimension d 128 d 512 Network Hierarchy LouvainNE RandNE LouvainNE RandNE Twitter2009 1h 21m 1h 57m 5h 49m 3h 47m 22h 59m Friendster 2h 31m 3h 17m 11h 26m 5h 36m 45h 24m MOLIERE 4h 44m 5h 5m 17h 57m 6h 10m 71h 13m Total execution time (inthan hours) LouvainNE is 4-5 times faster the fastest baseline RandNE for d 128 (7-12 times for d 512) Hierarchy construction step takes significant part of overall running time of 38 LouvainNE ( 70% for d 128) DYNAMICS ON AND OF COMPLEX NETWORKS 2020 18/09/2020 38

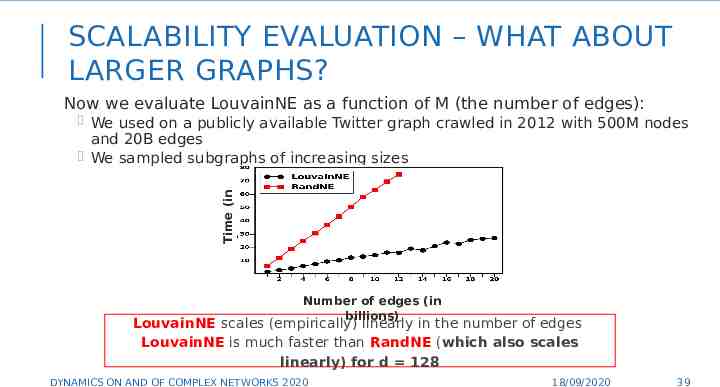
SCALABILITY EVALUATION – WHAT ABOUT LARGER GRAPHS? Now we evaluate LouvainNE as a function of M (the number of edges): Time (in hours) We used on a publicly available Twitter graph crawled in 2012 with 500M nodes and 20B edges We sampled subgraphs of increasing sizes Number of edges (in billions) LouvainNE scales (empirically) linearly in the number of edges LouvainNE is much faster than RandNE (which also scales linearly) for d 128 DYNAMICS ON AND OF COMPLEX NETWORKS 2020 18/09/2020 39 39

DOWNSTREAM TASK 1: NETWORK RECONSTRUCTION Evaluate whether learned embedding vectors of LouvainNE can reconstruct the graph G Idea: vectors of connected node pairs (link) should be more similar than vectors of non-connected node pairs (no link) We use AUC and precision@k 40 DYNAMICS ON AND OF COMPLEX NETWORKS 2020 18/09/2020 40

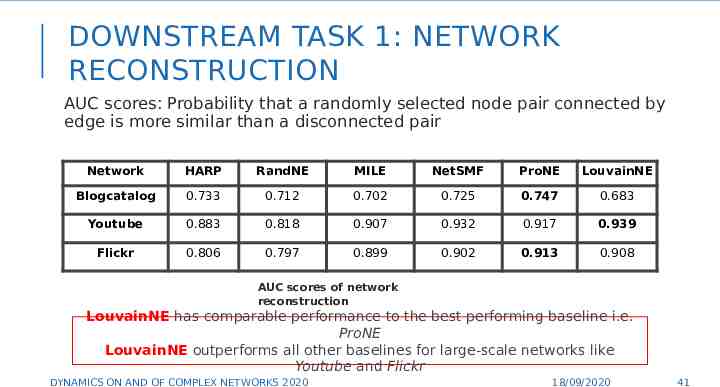
DOWNSTREAM TASK 1: NETWORK RECONSTRUCTION AUC scores: Probability that a randomly selected node pair connected by edge is more similar than a disconnected pair Network HARP RandNE MILE NetSMF ProNE LouvainNE Blogcatalog 0.733 0.712 0.702 0.725 0.747 0.683 Youtube 0.883 0.818 0.907 0.932 0.917 0.939 Flickr 0.806 0.797 0.899 0.902 0.913 0.908 AUC scores of network reconstruction LouvainNE has comparable performance to the best performing baseline i.e. ProNE LouvainNE outperforms all other baselines for large-scale networks like Youtube and Flickr DYNAMICS ON AND OF COMPLEX NETWORKS 2020 18/09/2020 41 41

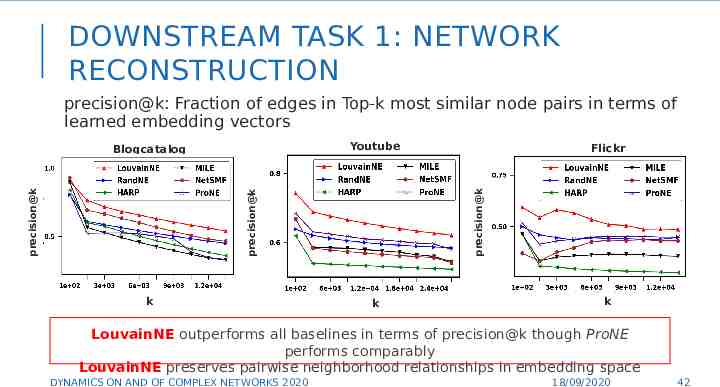
DOWNSTREAM TASK 1: NETWORK RECONSTRUCTION precision@k: Fraction of edges in Top-k most similar node pairs in terms of learned embedding vectors Youtube k Flickr precision@k precision@k precision@k Blogcatalog k k LouvainNE outperforms all baselines in terms of precision@k though ProNE performs comparably LouvainNE preserves pairwise neighborhood relationships in embedding space 42 DYNAMICS ON AND OF COMPLEX NETWORKS 2020 18/09/2020 42

DOWNSTREAM TASK 2: MULTI-LABEL CLASSIFICATION Evaluate whether learned embedding vectors of LouvainNE can help classify nodes Apply the generated embedding vectors as features in a supervised learning framework Classify a node into corresponding ground truth label(s) Multi-label classifier trained on Logistic Regression model Micro-F1 scores reported Network #Nodes #Edges Labels Density Blogcatalog [2] 10312 333983 39 5.5e 3 We only apply it on network with a labelled ground-truth Youtube [3] 1138499 2990443 47 4.6e 6 Flickr [3] 1715255 15555042 195 1.05e 5 DYNAMICS ON AND OF COMPLEX NETWORKS 2020 18/09/2020 43 43

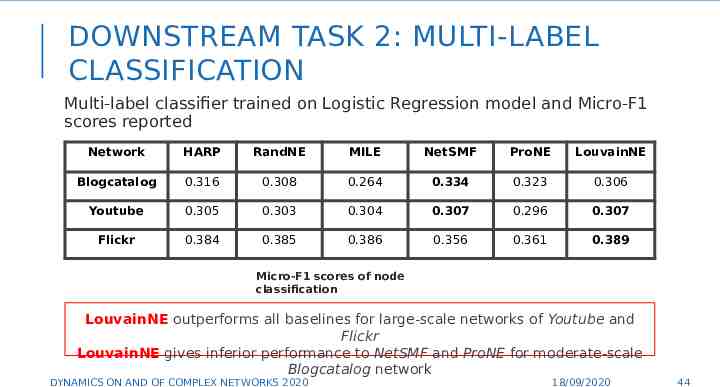
DOWNSTREAM TASK 2: MULTI-LABEL CLASSIFICATION Multi-label classifier trained on Logistic Regression model and Micro-F1 scores reported Network HARP RandNE MILE NetSMF ProNE LouvainNE Blogcatalog 0.316 0.308 0.264 0.334 0.323 0.306 Youtube 0.305 0.303 0.304 0.307 0.296 0.307 Flickr 0.384 0.385 0.386 0.356 0.361 0.389 Micro-F1 scores of node classification LouvainNE outperforms all baselines for large-scale networks of Youtube and Flickr LouvainNE gives inferior performance to NetSMF and ProNE for moderate-scale 44 Blogcatalog network DYNAMICS ON AND OF COMPLEX NETWORKS 2020 18/09/2020 44

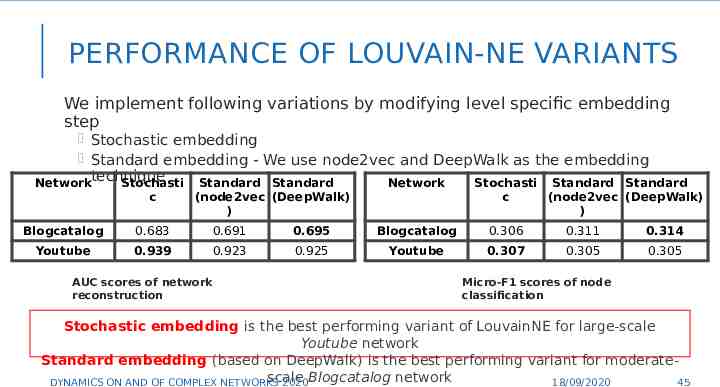
PERFORMANCE OF LOUVAIN-NE VARIANTS We implement following variations by modifying level specific embedding step Stochastic embedding Standard embedding - We use node2vec and DeepWalk as the embedding technique Network Stochasti Standard Standard Network Stochasti Standard Standard c (node2vec (DeepWalk) ) c (node2vec (DeepWalk) ) Blogcatalog 0.683 0.691 0.695 Blogcatalog 0.306 0.311 0.314 Youtube 0.939 0.923 0.925 Youtube 0.307 0.305 0.305 AUC scores of network reconstruction Micro-F1 scores of node classification Stochastic embedding is the best performing variant of LouvainNE for large-scale Youtube network Standard embedding (based on DeepWalk) is the best performing variant for moderate45 scale Blogcatalog network DYNAMICS ON AND OF COMPLEX NETWORKS 2020 18/09/2020 45

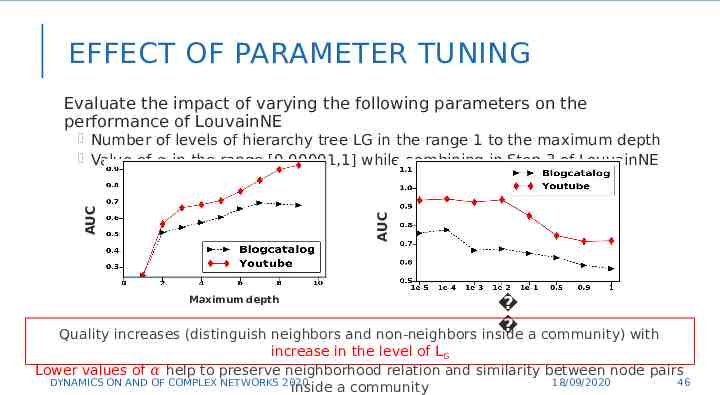
EFFECT OF PARAMETER TUNING Evaluate the impact of varying the following parameters on the performance of LouvainNE AUC AUC Number of levels of hierarchy tree LG in the range 1 to the maximum depth Value of 𝛼 in the range [0.00001,1] while combining in Step 3 of LouvainNE Quality increases (distinguish neighbors and non-neighbors inside a community) with Maximum depth increase in the level of LG 46 Lower values of 𝛼 help to preserve neighborhood relation and similarity between node pairs DYNAMICS ON AND OF COMPLEX NETWORKS 2020 18/09/2020 46 inside a community

CONCLUSION Proposed a fast and scalable embedding framework relying on community hierarchy Used the Louvain algorithm for fast construction of hierarchy of subgraphs Proposed model is flexible Level specific embedding step can accommodate multiple embedding techniques Evaluated the model on several real-world networks of different scales Our model is very fast and scales linearly with number of links even for massive-scale graphs Validated quality of generated embeddings on multiple downstream tasks 47 DYNAMICS ON AND OF COMPLEX NETWORKS 2020 18/09/2020 47

FUTURE WORK Evaluate on more variants Other community detection algorithms (those whose scale consensus) Compare different embeddings with the same technique Embed in hyperbolic space? 48 DYNAMICS ON AND OF COMPLEX NETWORKS 2020 18/09/2020 48

QUESTIONS? Code: https://github.com/maxdan94/LouvainNE 49 DYNAMICS ON AND OF COMPLEX NETWORKS 2020 18/09/2020 49