Chapter 9

Chapter 9

Non-degenerate Perturbation Theory Problem : H n En n can't solve exactly. But 0 H H H ' 2 H " with 0 Lim 0 H n0 En0 n0 Unperturbed eigenvalue problem. Can solve exactly. 0 0 Therefore, know E n and n . H ' 2 H " called perturbations Copyright – Michael D. Fayer, 2018

Solutions of 0 H n0 En0 n0 complete, orthonormal set of ket vectors 0 n 00 , 10 , 20 0 0 0 with eigenvalues E0 , E1 , E2 , and n0 m0 mn Kronecker delta 1 n m nm 0 n m Copyright – Michael D. Fayer, 2018

Expand wavefunction n n0 n 2 n and En En0 En 2 En also have 0 H H H ' 2 H " Have series for H n En Substitute these series into the original eigenvalue equation H n En n Copyright – Michael D. Fayer, 2018

Sum of infinite number of terms for all powers of l equals 0. H 0 0 n0 En0 n0 0 H n H ' n0 En0 n En' n0 0 H n H ' n H " n0 En0 n En n En n0 2 0 Coefficients of the individual powers of l must equal 0. zeroth order - l0 H n0 En0 n0 0 first order - l1 H n H ' n0 En0 n En n0 0 second order - l2 H n H ' n H " n0 En0 n En n En n0 0 0 0 0 Copyright – Michael D. Fayer, 2018

First order correction 0 H n En0 n E n H ' n0 Want to find E n and n . Expand n also substituting n ci i0 i Then 0 0 H n ci H i0 ci Ei0 i0 i Substituting this result. i After substitution c E i i 0 i En0 i0 En H ' n0 Copyright – Michael D. Fayer, 2018

After substitution c E i 0 i En0 i0 En H ' n0 i Left multiply by n0 n0 0 0 0 0 0 c E E E H ' i i n i n n n i c E i 0 i E n0 n0 i0 n0 En H ' n0 i n0 i0 0 unless n i, but then E n0 E n0 0 Therefore, the left side is 0. Copyright – Michael D. Fayer, 2018

We have n0 En H ' n0 0 n0 En n0 n0 H ' n0 0 E n number, kets normalized, and transposing, E n n0 H ' n0 The first order correction to the energy. 0 (Expectation value of H in zeroth order state n ) Then En En0 En and En Absorbing l into H nn En En0 En En n0 H ' n0 Hnn The first order correction to the energy is the expectation value of H ' . Copyright – Michael D. Fayer, 2018

First order correction to the wavefunction Again using the equation obtained after substituting series expansions c E i 0 i En0 i0 En H ' n0 i 0j Left multiply by 0j c E i 0 i En0 i0 0j En H ' n0 i Equals zero unless i j. c j E 0j En0 0j En H ' n0 c j E 0j En0 0j H ' n0 cj 0j H ' n0 E 0 n E 0 j j n Coefficients in expansion of ket in terms of the zeroth order kets. Copyright – Michael D. Fayer, 2018

cj cj 0j H ' n0 E 0 n E 0 j H 'jn E 0 n E 0 j j n H 'jn is the bracket of H ' with 0j and n0 . correction to zeroth order ket Therefore n 0 n H jn 0 ' j 0 0 j ( En E j ) The prime on the sum mean j n. zeroth order ket energy denominator Copyright – Michael D. Fayer, 2018

First order corrections E n En0 Hnn' n 0 n H jn 0 ' j 0 0 j ( En E j ) Hnn' n0 H n0 H jn 0j H n0 Copyright – Michael D. Fayer, 2018

Second Order Corrections Using l2 coefficient Expanding n n Substituting and following same type of procedures yields E n ' i H ni H in H nn 0 0 En Ei Second order correction due to first order piece of H. l2 coefficients have been absorbed. H ni H in n0 H i0 i0 H n0 Second order correction due to an additional second order piece of H. H mn H kn H km H nn n ' ' 0 0 0 En E k0 En0 Em0 k m E E n k Second order correction due to first order piece of H. k0 2 H ' 0 kn 0 k0 k ( En Ek ) Second order correction due to an additional second order piece of H. Copyright – Michael D. Fayer, 2018

Energy and Ket Corrected to First and Second Order H ni H in ' H nn E E H 'nn 0 0 En Ei i 0 n 0 n H jn ' 0 0 ( E E ) j n j 0 j H mn H kn H km H nn ' ' 0 0 0 0 0 0 En Ek En Em k m E E n k k0 2 H ' 0 kn 0 k0 k ( En Ek ) Copyright – Michael D. Fayer, 2018

Example: x3 and x4 perturbation of the Harmonic Oscillator E x Vibrational potential of molecules not harmonic. Approximately harmonic near potential minimum. Expand potential in power series. First additional terms in potential after x2 term are x3 and x4. Copyright – Michael D. Fayer, 2018

H p 2 1 2 3 4 k x cx qx 2m 2 quartic “force constant” cubic “force constant” p 2 1 2 H kx 2m 2 0 1 0 H aa a a 2 harmonic oscillator – know solutions 1 E 0 n 0 2 zeroth order eigenvalues n zeroth order eigenkets 3 H ' c x q x 4 perturbation c and q are expansion coefficients like l. When c and q 0, H H 0 Copyright – Michael D. Fayer, 2018

n H' n H nn 3 4 n cx qx n 3 4 c n x n q n x n In Dirac representation 0 x 2k 1 2 a a First consider cubic term. 3 x a a 3 Multiply out. Many terms. 3 2 3 a , a a , aa a , a . None of the terms have the same number of raising and lowering operators. 3 n x n 0 (At second order will not be zero.) Copyright – Michael D. Fayer, 2018

2 02 n x n 2 n a a 4k 4 a a 4 n has terms with same number of raising and lowering operators. Therefore, Using 4 4 n x n 0 a n n1/ 2 n 1 and a n ( n 1)1/ 2 n 1 n aaa a n n 1 n 2 n a a aa n n n 1 n aa aa n n 1 2 n a aa a n n2 Only terms with the same number of raising and lowering operators are non-zero. There are six terms. n aa a a n n n 1 n a aaa n n 1 n Copyright – Michael D. Fayer, 2018

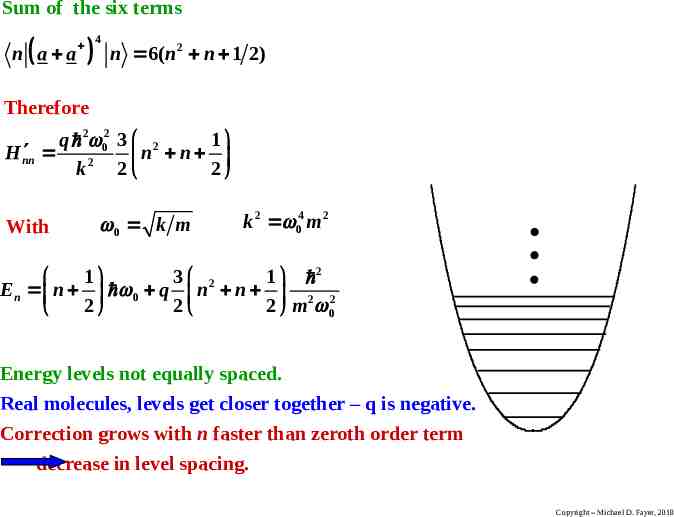
Sum of the six terms n a a 4 n 6( n2 n 1 2) Therefore q 2 02 3 2 1 H nn n n k 2 2 2 With 0 k m k 2 04 m 2 1 3 2 1 2 En n 0 q n n 2 2 2 2 2 m 0 Energy levels not equally spaced. Real molecules, levels get closer together – q is negative. Correction grows with n faster than zeroth order term decrease in level spacing. Copyright – Michael D. Fayer, 2018

Perturbation Theory for Degenerate States H 1 E 1 1 normalize and orthogonal H 2 E 2 1 and 2 and 2 Degenerate, same eigenvalue, E. If c1 1 c2 2 with c1c1 c2 c2 1 H E Any superposition of degenerate eigenstates is also an eigenstate with the same eigenvalue. Copyright – Michael D. Fayer, 2018

n linearly independent states with same eigenvalue system n-fold degenerate Can form n orthonormal i from the n degerate n . Can form an infinite number of sets of i . Nothing unique about any one set of n degenerate eigenkets. Copyright – Michael D. Fayer, 2018

Want approximate solution to H 0 H ' j E j j zeroth order Hamiltonian 0 perturbation 0 H 0j E 0j 0j zeroth order eigenket zeroth order energy But E i0 is m-fold degenerate. Call these m eigenkets belonging to the m-fold degenerate E10 10 , 20 m0 orthonormal With E10 E20 Em0 E10 Copyright – Michael D. Fayer, 2018

Here is the difficulty 0 i i0 perturbed ket 0 But, i 0 zeroth order ket having eigenvalue, E1 0 is a linear combination of the i . i0 c1 10 c2 20 cm m0 We don’t know which particular linear combination it is. i0 is the correct zeroth order ket, but we don’t know the ci. The correct zero order ket depends on the nature of the perturbation. p states of the H atom in external magnetic field – p1, p0, p-1 electric field – px, pz, py Copyright – Michael D. Fayer, 2018

To solve problem Expand E and i E E10 E m i c j 0j i j 1 Some superposition, but we don’t know the cj. Don’t know correct zeroth order function. Substituting the expansions for E and i into 0 H H ' i Ei i and obtaining the coefficients of powers of l, gives zeroth order H first order H 0 m cj 0 j 0 1 E j 1 0 0 1 E m 0 c j j j 1 m c E H ' i j 0 j j 1 want these Copyright – Michael D. Fayer, 2018

H 0 0 1 E m c E H ' i j 0 j To solve j 1 0 substitute i Ak k k Need H ' 0j 0 0 Use projection operator k k H ' 0j k0 k0 H ' 0j k 0 The projection operator gives the piece of H ' j 0 that is k . 0 0 Then the sum over all k gives the expansion of H ' j in terms of the i . 0 0 Defining H kj' k H ' j Known – know perturbation piece of the Hamiltonian and the zeroth order kets. H ' 0j H kj k0 k Copyright – Michael D. Fayer, 2018

H 0 0 1 E m c E H ' i j H ' 0j H kj k0 0 j k j 1 this piece becomes m c H j m 0 j c j H kj k0 j 1 j 1 k 0 Substituting this and i Ak k gives k E 0 k 0 1 E Ak k 0 k m E c j j 1 0 j m 0 c j H kj k k j 1 Result of operating H0 on the zeroth order kets. Left multiplying by i0 E k 0 k 0 1 0 i E Ak 0 k m 0 i E c j j 1 0 j m 0 0 c j H kj i k k j 1 Copyright – Michael D. Fayer, 2018

E 0 k 0 1 0 i E Ak k 0 k m 0 i E c j 0 j j 1 m 0 0 c j H kj i k k j 1 Correction to the Energies Two cases: i m (the degenerate states) and i m. i m Left hand side – sum over k equals zero unless k i. But with i m, E i0 E10 Therefore, Ei0 E10 0 The left hand side of the equation 0. Right hand side, first term non-zero when j i. Bracket 1, normalization. Second term non-zero when k i. Bracket 1, normalization. The result is m H c ij j E ci 0 j 1 We don’t know the c’s and the E s . Copyright – Michael D. Fayer, 2018

m H c ij j E ci 0 is a system of m of equations for the cj’s. j 1 H11 E c1 H12 c2 H1 m cm 0 c1 H 22 E c2 H 2 m cm 0 H 21 One equation for each index i of ci. E cm 0 H m 1c1 H m 2 c2 H mm Besides trivial solution of c1 c2 cm 0 only get solution if the determinant of the coefficients vanish. H11 E H12 H 22 E H m 1 H1 m H m 2 H 2 m E H mm 0 We know the H jk 0j H k0 Have mth degree equation for the E s . Copyright – Michael D. Fayer, 2018

Solve mth degree equation – get the E i s . Now have the corrections to energies. To find the correct zeroth order eigenvectors, one for each E i , substitute E i (one at a time) into system of equations. Get system of equations for the coefficients, cj’s. H11 E i c1 H 12 c2 H1 m cm 0 Know the H ij . c1 H 22 E i c2 H 2 m cm 0 H 21 Ei cm 0 H m 1c1 H m 2 c2 H mm There are only m – 1 conditions because can multiply everything by constant. Use normalization for mth condition. c1*c1 , c2*c2 , cm* cm 1 Now we have the correct zeroth order functions. Copyright – Michael D. Fayer, 2018

The solutions to the mth degree equation (expanding determinant) are E1, E 2, E m Therefore, to first order, the energies of the perturbed initially degenerate states are E i E10 Ei 1 i m Have m different E i s (unless some still degenerate). With E i E10 as 0 Copyright – Michael D. Fayer, 2018

Correction to wavefunctions Again using equation found substituting the expansions into the first order equation E k 0 k m E10 Ak k0 E c j 0j j 1 m 0 c j H kj k k j 1 Left multiply by i0 gives 1 i k m gives 0 Orthogonality makes other terms zero. Normalization gives 1 for non-zero brackets. E 0 k 0 1 E A k m c j H kj j 1 m c H j Therefore Ak kj j 1 E 0 1 E 0 k k m Normalization gives Aj 0 for j m. Already have part of wavefunction for j m Copyright – Michael D. Fayer, 2018

First order degenerate perturbation theory results E i E10 Ei m c H j i i0 k m kj j 1 E 0 1 E k0 k0 Correct zeroth order function. Coefficients ck determined from system of equations. Correction to zeroth order function. Copyright – Michael D. Fayer, 2018