Chapter 7 Linear Programming I. Simplex Method Ding-Zhu Du

Chapter 7 Linear Programming I. Simplex Method Ding-Zhu Du

LP examples A post office requires different numbers of full-time employees on different days of the week. The number of full-time employees required on each day is given in the table. Union rules state that each full-time employee must work five consecutive days and then receive two days off. The post office wants to meet its daily requirements using only fulltime employees. Formulate an LP that the post office can use to minimize the number of full-time employees that must be hired.

Optimal occurs at a vertex!!! z 4 x 5 y 2 x 3 y 60 Feasible domain

Slack Form min ax z 4 x 5 y s.t. 2 x 3 y w 60 x 0, y 9, w 0. min x z cx s.t. Ax b x 0. rank ( A) m.

What’s a vertex? A point x in a polyhadren is called a vertex if 1 x ( y z ), y, z x y z. 2

Fundamental Theorem Let {x Ax b, x 0}. If min cx over x has an optimal solution, then it can be found in vertices of .

Proof. Consider an optimal solution x * with maximum number of zero components among all optimal solutions. We will show that x * is a vertex of . By contradition, suppose x * is not, that is, there exist y, z such that x* ( y z ) / 2 and x*, y, z are distinct. Since cx* cy, cx* cz, and cx* (cy cz ) / 2, we must have cx* cy cz. This means that y and z are also optimal solutions. It follows that all feasible points on line x* ( y-x*) are optimal solutions. However, does not contain any line. Thus, the line must have a point x' not in , that is, x' violates at least one constraint.

Proof (cont’s). Note that for any , A( x* ( y-x*)) b. Thus, x' cannot violate constraint Ax b. Moreover, for xi* 0, since xi* ( yi zi ) / 2 and yi ,zi 0, we must have zi yi xi * 0. Therefore, the ith component of x* ( y-x*) is equal to 0 for any . This means that x' cannot violate constraint xi 0. Hence, x' must violate a constraint x j 0 for some j with x j* 0. Now, we can easily find an optimal solution between x' and x*, which has one more zero - component than x*, a contradiction.

Characterization of Vertex Let a j denote the jth column of A. Then a feasible point x is a vertex if and only if all a j for 1 j n with x j 0 are linearly independent.

Proof If a j for x j 0 are linearly independent, then x j are uniquely determined by index set { j x j 0}. If a j for x j 0 are not linearly independent, then there exists j for j with x j 0 such that x 0 j a j 0 and not all j j are zero. Define d (d j ) by setting j if x j 0 d j 0 if x j 0. Then d 0 and for sufficiently small 0, y z y x d , z x d and x . 2

Basic Feasible Solution A vertex is also called a basic feasible solution. The index set of a maximum independent subset of column vectors called a basis. A basis is feasible if there exists a basic feasible solution x such that I { j x j 0}. Denote AI (a j , j I ). Then an index subset I is a feasible basis if and only if rank ( AI ) m I and AI 1b 0.

Optimality Condition Each feasible basis I is associated with a basic feasible solution x with xI AI 1b and xI 0 where I { j j I }. Moreover, x is optimal if and only if 1 I cI cI A AI 0 under nondegeneracy condition.

Sufficiency Ax b AI xI AI xI b 1 I 1 I xI A b A AI xI 1 I 1 I cx cI xI cI xI cI A b (cI cI A AI ) xI 1 I Since cI cI A AI 0 and xI 0, cx reaches the minimum at xI 0.

Nondegeneracy Assumption 1 I For every feasible basis I , A b 0. Remark Under nondegeneracy condition, every feasible basis is associated with exactly one feasible basic solution.

Necessary 1 I Denote c' I cI cI A AI . Assume for some j* I , c' j* 0. We show that 1 x I AI b is not optimal. x x I 0 1 1 Denote (aij ) AI A and b' AI b. Case 1. aij* 0 for all i 1,2,., m.

Case 1. aij* 0 for all i 1,2,., m. Then for any 0, x ( ) j 0 if j I and j j * if j j * b' a if j I and a 1 ij i ij* is a feasible solution. Hence, the object function value goes to as . 1 I So, xI 0 and xI A b do not give an optimal solution.

Case 2. aij * 0 for some i 1,2,., m. Choose i * such that bi bi* min aij * 0 . ai* j* aij Let j ' I with ai* j ' 1. (pivoting) Set I ' ( I \ { j '}) { j*}. Then I ' is a new feasible basis with basic feasible solution of object function value b'i* c I b c' j* cI b ai* j* since b'i* 0 by nondegeneracy assumption .

Simplex Method The proof of necessarity gives a method to solve the linear propromming, called simplex method.

Simplex Table min z 3x1 x2 2 x3 s.t. x1 x2 3 x3 x4 30 2 x1 2 x2 5 x3 x5 24 4 x1 x2 2 x3 x6 36 x1 , x2 , x3 , x4 , x5 , x6 0 z 3 1 2 30 1 24 2 36 4 1 2 1 3 5 2 0 0 0 1 0 0 0 1 0 0 0 1

I 0 {4,5,6} z 3 1 2 30 1 1 3 24 2 2 5 36 4 1 2 1 1 1

I1 ({4,5,6} \ {5}) {2} z 3 1 2 30 1 1 3 1 12 1 1 5/2 1/2 36 4 1 2 1

I1 ({4,5,6} \ {5}) {2} z 12 2 18 0 12 1 24 3 0 0 1 0 1/2 1/2 1/2 1 1 / 2 5/2 1/2 1/ 2 1/2 1

I1 {4,2,6} z 12 2 18 0 12 1 24 3 0 0 1 0 1/2 1/2 1/2 1 1 / 2 5/2 1/2 1/ 2 1/2 1

I 2 ({4,2,6} \ {6}) {1} z 12 2 18 0 12 1 8 1 0 0 1 0 1/2 1/2 1/2 1 1 / 2 5/2 1/2 1/ 6 1/6 1/3

I 2 {4,2,1} z 28 18 4 8 0 0 0 1 0 1/6 1/6 0 1/2 1 1 / 2 1 8/3 2/3 0 1/ 6 1/6 2/3 1/ 3 1/3

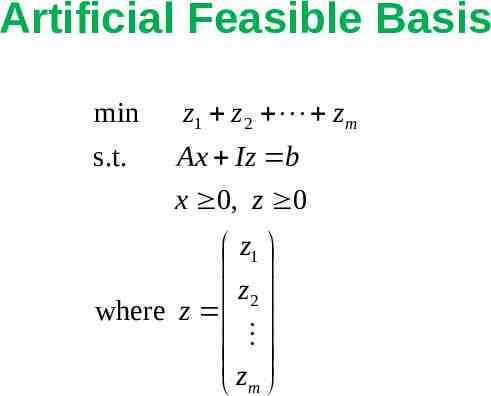
Puzzle 1 How do we find the 1st basic feasible solution or the 1st feasible basis ?

Artificial Feasible Basis min z1 z 2 z m s.t. Ax Iz b x 0, z 0 z1 z2 where z z m

Puzzle 2 When nondegeneracy assumption does not hold, how to solve LP?

lexicographical ordering Consider two vectors x ( x1,x2 ,., xn ) and y ( y1,y2 ,.,yn ). x is said to be lexicographically larger than y, written as x L y, if x1 y1, ., xi 1 yi 1, xi yi for some 1 i n. A vector x is lexicographocally positive if x L 0.

Method Initially, rearrange the ordering of n columns such that the initial feasible basis is placed at the first m columns. This makes that every row in the initial simplex table except the top row is lexicographically positive.

Method(cont’) For choice of i' , we choose b'i ' a'i '1 a 'i 'n i' such that ( , , . ) is the lexicographocally smallest a 'i ' j ' a 'i ' j ' a'i ' j ' b'i a 'i1 a'in one among ( , , . ) for a'ij ' 0. a'ij ' a'ij ' a 'ij ' This choice guarantees that the lexicographically positveness of all rows other than the top row will be preserved under pivoting.

Method (cont’) Since all rows other than the top row are lexicographically positive, each pivot will make the top decreasse strictly in lexicographical ordering. Therefore, the above additional rules guarantee that the algorithm visit each feasible basis at most once and the objective function value is nonincreasing. Therefore, the algorithm either finds nonexistence of optimal solution or find an optimal feasible basic solution with feasible basis I such that c - cI AI 1 A 0.

Theorem If the linear programming has an optimal solution, then it has an optimal basic feasible solution associated with feasible basis I such that c - cI AI 1 A 0. Moreove, if a feasible basis I satisfies c - cI AI 1 A 0, then the basic feasible solution associated with I is optimal.

Puzzle 3 What is the running time of Simplex Method?

Complexity of LP Simplex Method runs in exponential time. Ellepsoid Method runs in O(n 6 ) time. Interior Point Method runs in O(n 3.5 ) time. Given an optimal solution, an optimal extreme point cn be computed in polynomial - time.

Thanks, End