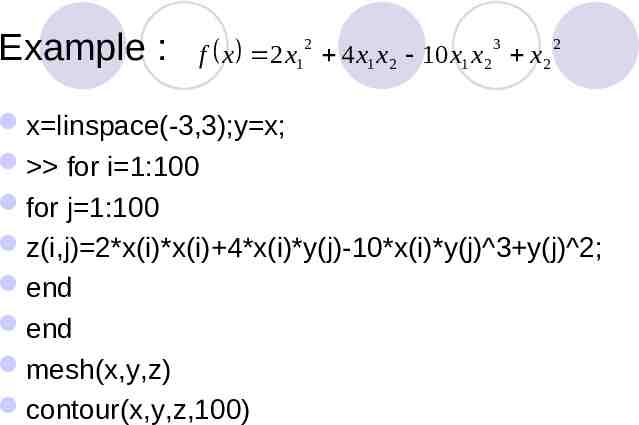Chapter 3 UNCONSTRAINED OPTIMIZATION Prof. S.S. Jang Department
46 Slides4.04 MB
Chapter 3 UNCONSTRAINED OPTIMIZATION Prof. S.S. Jang Department of Chemical Engineering National Tsing-Hua Univeristy
Contents Optimality Criteria Direct Search Methods Nelder and Mead (Simplex Search) Hook and Jeeves(Pattern Search) Powell’s Method (The Conjugated Direction Search) Gradient Based Methods Cauchy’s method (the Steepest Decent) Newton’s Method Conjugate Gradient Method (The Fletcher and Reese Method) Quasi-Newton Method – Variable Metric Method
3-1 The Optimality Criteria Given a function (objective function) f(x), where and let T f x f x * f x * x x * x1 x x 2 xN 1 x x * T 2 f x * x x * 3 x 2 f x * 0 Stationary Condition: Sufficient minimum criteria 2 Sufficient maximum criteria f x * negative definite 2 f x * positive definite
Definiteness A real quadratic for Q xTCx and its symmetric matrix C [cjk] are said to be positive definite (p.d.) if Q 0 for all x 0. A necessary and sufficient condition for p.d. is that all the determinants: c11 C1 c11 , C2 c21 c11 c12 c12 , C3 c21 c22 c22 c31 c32 c13 c23 ., Cn det C c33 are positive, C is negative definitive (n.d.) if –C is p.d.
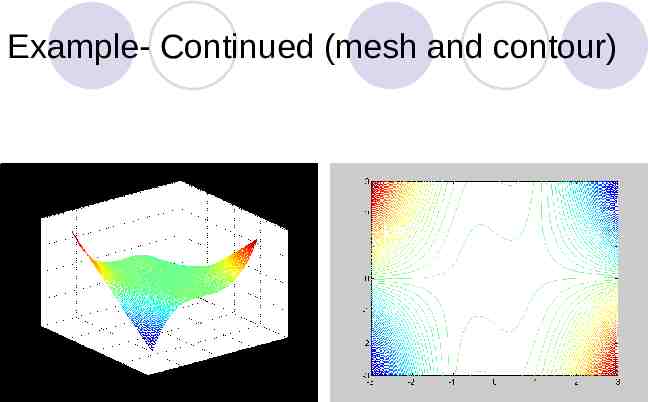
Example : 2 3 f x 2 x1 4 x1 x 2 10 x1 x 2 x 2 2 x linspace(-3,3);y x; for i 1:100 for j 1:100 z(i,j) 2*x(i)*x(i) 4*x(i)*y(j)-10*x(i)*y(j) 3 y(j) 2; end end mesh(x,y,z) contour(x,y,z,100)
Example- Continued (mesh and contour)
Example-Continued At 0 x* 0 f x1 x x* 2 f 2 x1 x x* 4 x x* 2 2 2 f x 2 2 2 f x1 x 2 4 x1 4 x 2 10 x 2 0 2 x x* 12 x 2 10 10 10 4 H 2 10 Indefinite, x* is a non-optimum point.
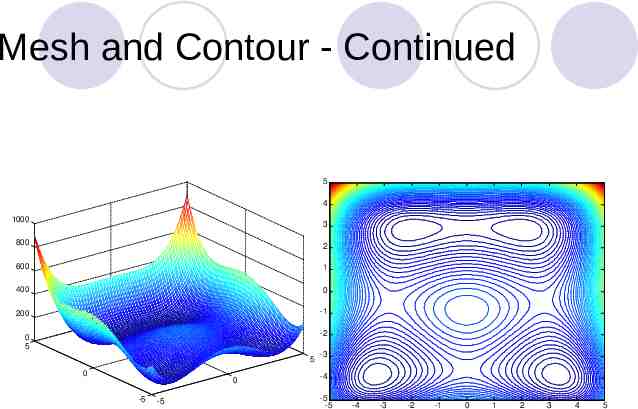
Mesh and Contour – Himmelblau’s function : f(x) (x12 x2-11)2 (x1 x22-7)2 Optimality Criteria may find a local minimum in this case x linspace(-5,5);y x; for i 1:100 for j 1:100 z(i,j) (x(i) 2 y(j)-11) 2 (x(i) y(j) 2-7) 2; end end mesh(x,y,z) contour(x,y,z,80)
Mesh and Contour - Continued 5 4 1000 3 800 2 600 1 400 0 200 -1 0 5 -2 5 0 0 -5 -5 -3 -4 -5 -5 -4 -3 -2 -1 0 1 2 3 4 5
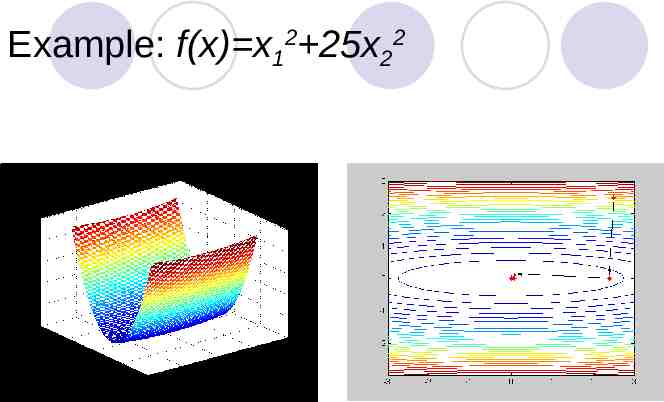
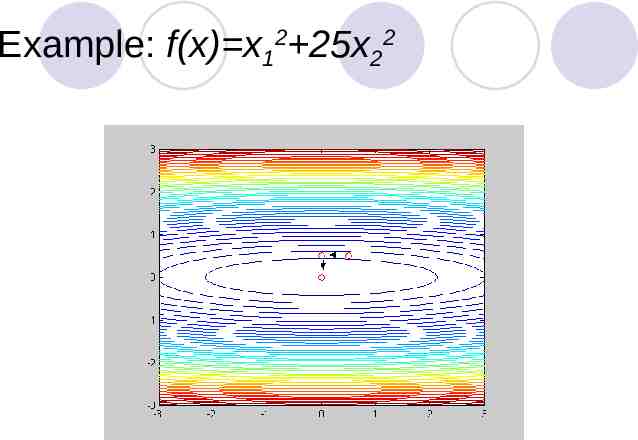
Example: f(x) x12 25x22
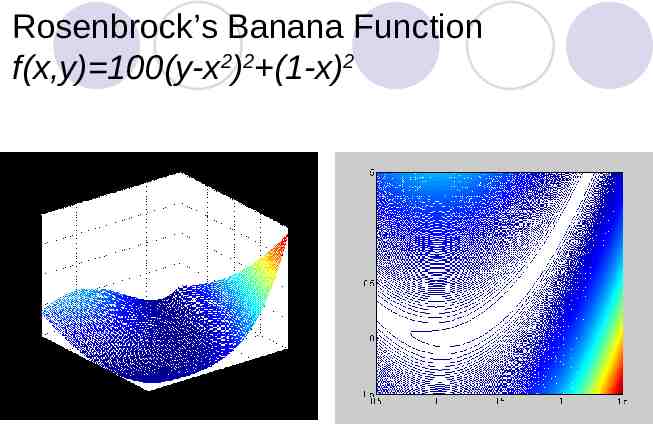
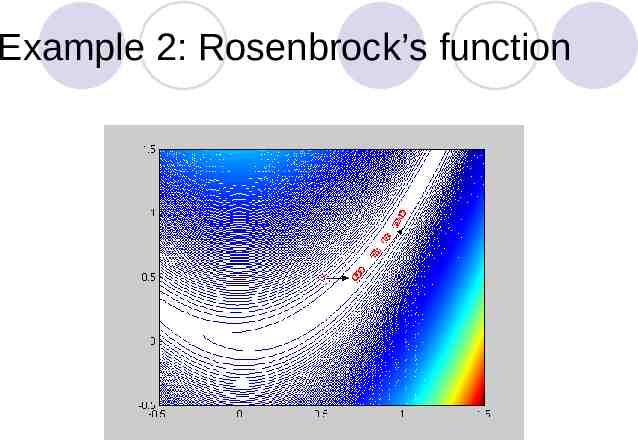
Rosenbrock’s Banana Function f(x,y) 100(y-x2)2 (1-x)2
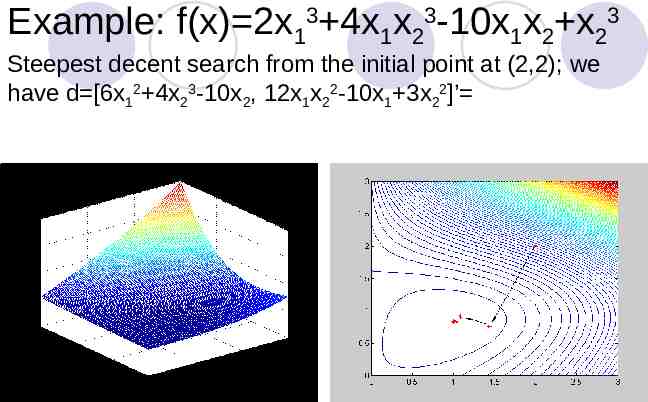
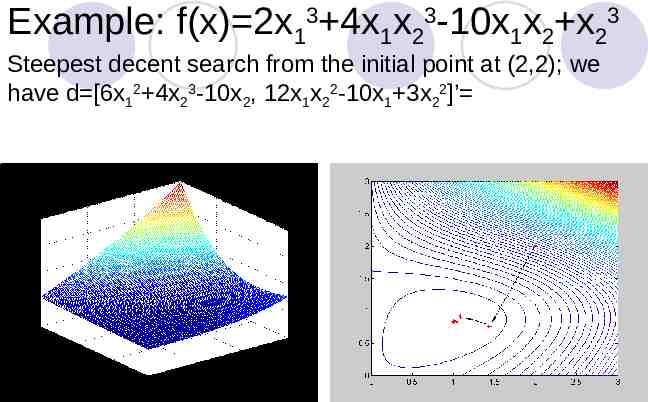
Example: f(x) 2x13 4x1x23-10x1x2 x23 Steepest decent search from the initial point at (2,2); we have d [6x12 4x23-10x2, 12x1x22-10x1 3x22]’
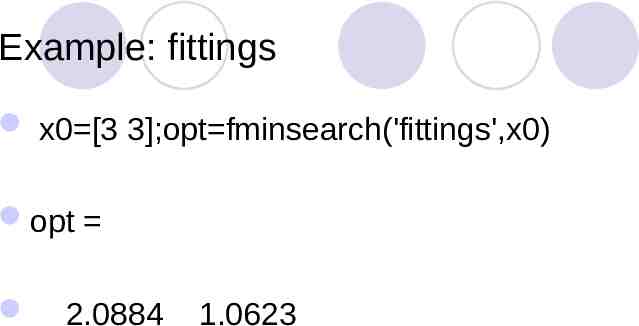
Example: Curve Fitting From the theoretical considerations, it is believe that the dependent variable y is related to variable x via a two-parameter function: k1 x y 1 k 2 x The parameters k1 and k2 are to be determined by a least square of the following experimental data: x y 1.0 2.0 3.0 4.0 1.05 1.25 1.55 1.59
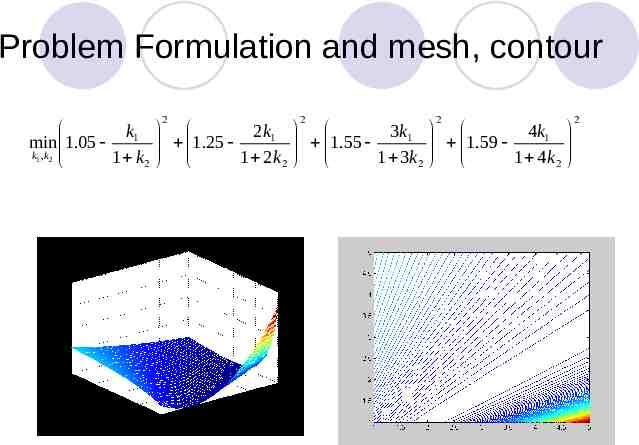
Problem Formulation and mesh, contour 2 2 2 k1 2k1 3k1 4k1 1.25 1.55 1.59 min 1.05 k1 , k 2 1 k2 1 2k 2 1 3k 2 1 4k 2 2
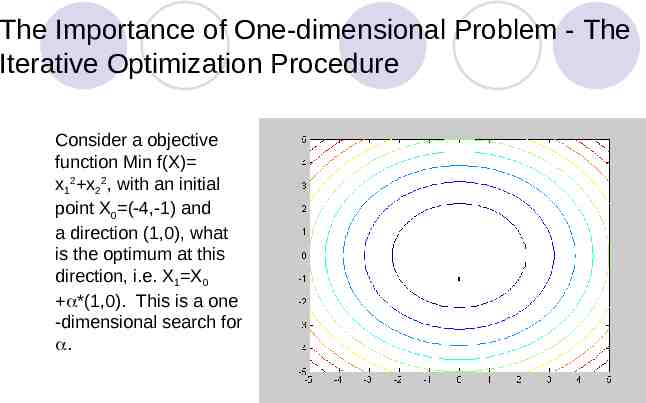
The Importance of One-dimensional Problem - The Iterative Optimization Procedure Consider a objective function Min f(X) x12 x22, with an initial point X0 (-4,-1) and a direction (1,0), what is the optimum at this direction, i.e. X1 X0 *(1,0). This is a one -dimensional search for .
3-2 Steepest Decent Approach – Cauchy’s Method A direction d [x1,x2,.,xn]’ is a ndimensional vector, a line search is an approach such that from a based point x0, find *, for all , x0 *d is an optimum. Theorem: the direction d -[ f/ x1, f/ x2, ., f/ xn]’ is the steepest decent direction. Proof: Consider a two dimensional system: f(x1,x2), the movement ds2 dx12 dx22, and f ( f/ x1)dx1 ( f/ x2)dx2 ( f/ x1)dx1 ( f/ x2)(ds2-dx12)1/2. Then to maximize the change f, we have d( f)/dx1 0. It can be shown that dx1/ds ( f/ x1)/( ( f/ x1)2 ( f/ x2)2)1/2, dx2/ds ( f/ x2)/( ( f/ x1)2 ( f/ x2)2)1/2
Example: f(x) 2x13 4x1x23-10x1x2 x23 Steepest decent search from the initial point at (2,2); we have d [6x12 4x23-10x2, 12x1x22-10x1 3x22]’
Quadratic Function Properties Property #1: Optimal linear search for a quadratic function: f ( x) f ( xk ) T f k x xk Let x xk sk df 0 T f k sk skT Hsk d T f k sk T sk Hsk 1 x xk T H x xk 2
Quadratic Function Properties- Continued Property #2 fk 1 is orthogonal to sk for a quadratic function 1 T Let f ( x) a x b x Hx 2 f b Hx or Hxk f k b T Since s T f s T H s 0 ( sk xk 1 xk ) skT f k skT H xk 1 xk 0 skT f k skT f k 1 b f k b 0 skT f k 1 0
3-2 Newton’s Method – Best Convergence approaching the optimum f ( x) f xk T f k x xk 1 x xk T H x xk 2 Let Δxk x xk ; Want d f x f xk 0 T f k H x xk xk xk 1 xk H 1 f k Define d H 1 f k xk 1 xk * H 1 f k
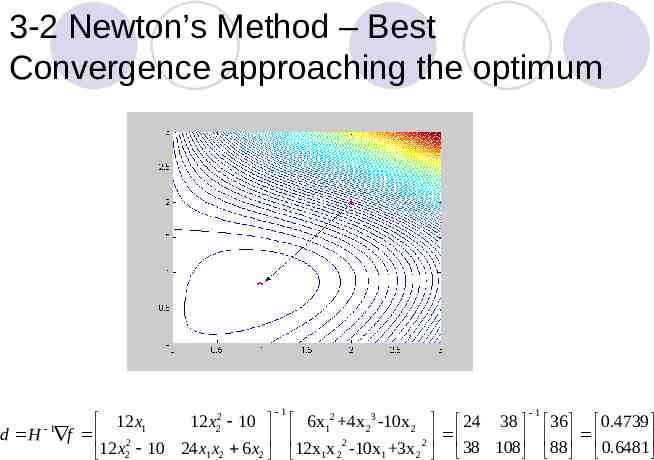
3-2 Newton’s Method – Best Convergence approaching the optimum 1 1 12 x1 12 x22 10 6x12 4x 23 -10x 2 24 38 36 0.4739 1 d H f 88 0.6481 2 2 2 38 108 12 x 10 24 x x 6 x 12x x -10x 3x 2 1 2 2 1 2 1 2
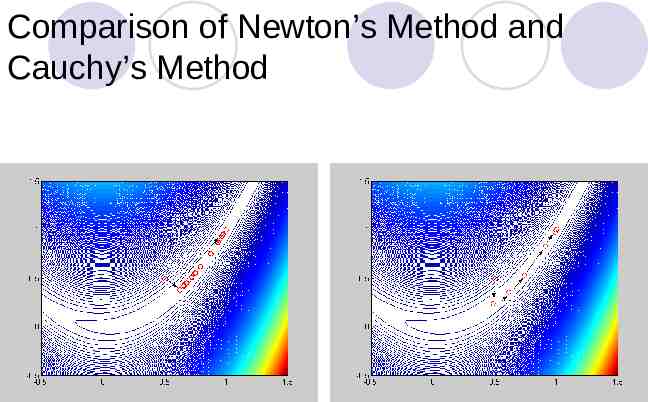
Comparison of Newton’s Method and Cauchy’s Method
Remarks Newton’s method is much more efficient than Steep Decent approach. Especially, the starting point is getting close to the optimum. There is a requirement for the positive definite of the hessian in implementing Newton’s method. Otherwise, the search will be diverse. The evaluation of hessian requires second derivative of the objective function, thus, the number of function evaluation will be drastically increased if a numerical derivative is used. Steepest decent is very inefficient around the optimum, but very efficient at the very beginning of the search.
Conclusion Cauchy’s method is very seldom to use because of its inefficiency around the optimum. Newton’s method is also very seldom to use because of the requirement of second derivative. A useful approach should be somewhere in between.
3-3 Method of Powell’s Conjugate Direction Definition: Let u and v denote two vectors in En. They are said to be orthogonal, if their scalar product equals to zero, i.e. u v 0. Similarly, u and v are said to be mutually conjugative with respect to a matrix A, if u and Av are mutually orthogonal, i.e. u Av 0. Theorem: If conjugate directions to the hessian are used to any quadratic function of n variables that has a minimum, can be minimized in n steps.
Powell’s Conjugated Direction MethodContinued Corollary: Generation of conjugated vectorsExtended Parallel Space Property Given a direction d and two initial point x (1), x(2), we assume: f ( x) a bx 1 x Hx q( x) T 2 (1) x x d then dq dq dx (b' x' H )d d dx d dq Assume, at y1 0 (b' y1 ' H )d (1) d Same approach, start from x ( 2 ) get y2 such that dq 0 (b' y2 ' H )d (1) d (1) - (2) yields y1 ' y2 ' Hd 0 y1 ' y2 ' is conjugated to d w.r.t. H
Powell’s Algorithm Step 1: Define x0, and set N linearly indep. Directions say: s(i) e(i) Step 2: Perfrom N 1 one directional searches along with s(N), s(1), ,s(N) Step 3: Form the conjugate direction d using the extended parallel space property. Step 4: Set s (1) s ( 2) , s ( 2) s (3) , , s ( N 1) s ( N ) , s ( N ) d Go to Step 2
Powell’s Algorithm (MATLAB) function opt powell n dim(x0,n,eps,tol,opt func) xx x0;obj old feval(opt func,x0);s zeros(n,n);obj obj old;df 100;absdx 100; for i 1:n;s(i,i) 1;end while df eps/absdx tol x old xx; for i 1:n 1 if(i n 1) j 1; else j i; end ss s(:,j); alopt one dim pw(xx,ss',opt func); xx xx alopt*ss'; if(i 1) y1 xx; end if(i n 1) y2 xx; end end d y2-y1; nn norm(d,'fro'); for i 1:n d(i) d(i)/nn; end dd d'; alopt one dim pw(xx,dd',opt func); xx xx alopt*d dx xx-x old; plot(xx(1),xx(2),'ro') absdx norm(dx,'fro'); obj feval(opt func,xx); df abs(obj-obj old); obj old obj; for i 1:n-1 s(:,i) s(:,i 1); end s(:,n) dd; end opt xx
Example: f(x) x12 25x22
Example 2: Rosenbrock’s function
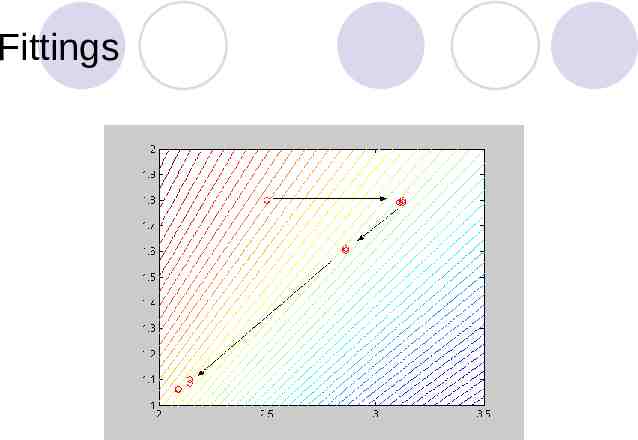
Example: fittings x0 [3 3];opt fminsearch('fittings',x0) opt 2.0884 1.0623
Fittings
Function Fminsearch help fminsearch FMINSEARCH Multidimensional unconstrained nonlinear minimization (Nelder-Mead). X FMINSEARCH(FUN,X0) starts at X0 and finds a local minimizer X of the function FUN. FUN accepts input X and returns a scalar function value F evaluated at X. X0 can be a scalar, vector or matrix. X FMINSEARCH(FUN,X0,OPTIONS) minimizes with the default optimization parameters replaced by values in the structure OPTIONS, created with the OPTIMSET function. See OPTIMSET for details. FMINSEARCH uses these options: Display, TolX, TolFun, MaxFunEvals, and MaxIter. X FMINSEARCH(FUN,X0,OPTIONS,P1,P2,.) provides for additional arguments which are passed to the objective function, F feval(FUN,X,P1,P2,.). Pass an empty matrix for OPTIONS to use the default values. (Use OPTIONS [] as a place holder if no options are set.) [X,FVAL] FMINSEARCH(.) returns the value of the objective function, described in FUN, at X. [X,FVAL,EXITFLAG] FMINSEARCH(.) returns a string EXITFLAG that describes the exit condition of FMINSEARCH. If EXITFLAG is: 1 then FMINSEARCH converged with a solution X. 0 then the maximum number of iterations was reached. [X,FVAL,EXITFLAG,OUTPUT] FMINSEARCH(.) returns a structure OUTPUT with the number of iterations taken in OUTPUT.iterations. Examples FUN can be specified using @: X fminsearch(@sin,3) finds a minimum of the SIN function near 3. In this case, SIN is a function that returns a scalar function value SIN evaluated at X. FUN can also be an inline object: X fminsearch(inline('norm(x)'),[1;2;3]) returns a minimum near [0;0;0]. FMINSEARCH uses the Nelder-Mead simplex (direct search) method. See also OPTIMSET, FMINBND, @, INLINE.
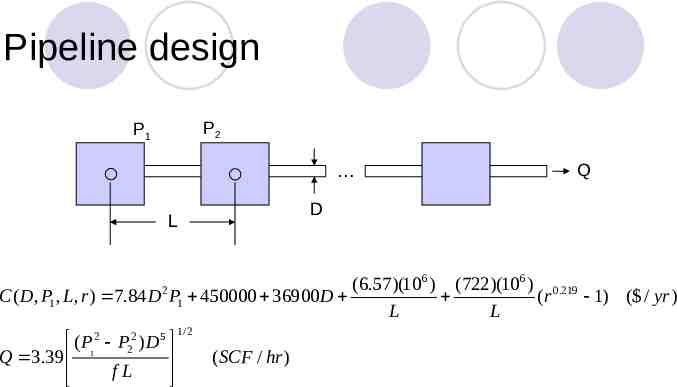
Pipeline design P2 P1 Q D L (6.57)(106 ) (722)(106 ) 0.219 C ( D, P1 , L, r ) 7.84 D P1 450000 36900 D (r 1) ( / yr ) L L 2 ( P12 P22 ) D 5 Q 3.39 f L 1/ 2 ( SCF / hr )
3-4 Conjugated Gradient Method Fletcher-Reeves’s Method (FRP) Given s1 - f1, s2 - f2 s1 It can be shown that if f 2T f 2 T f1 f1 where, s2 is started at the optimum of the line search along the direction s1. And f a bTxk 1/2xkTHxk, then s2 is conjugated to s1 with respect to H (k ) 2 g ( k 1) Most general iteration: s ( k ) g ( k ) s ( k 1) 2 g
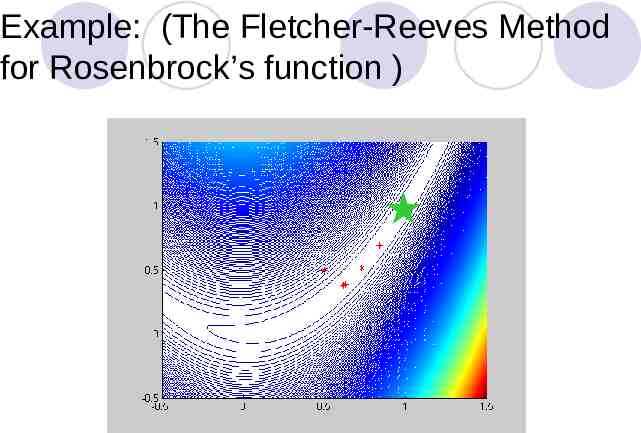
Example: (The Fletcher-Reeves Method for Rosenbrock’s function )
3-5 Quasi-Newton’s Method (Variable Matrix Method) The variable matric approach is using an approximate Hessian matrix without taking second derivative of the objective function, the Newton’s direction can be approximated by: xk 1 xk- kAk fk As Ak I Cauchy’s direction As Ak H-1 Newton’s direction In the variable matric approach, Ak can be updated to approximate the inverse of the Hessian by iterative approaches
3-5 Quasi-Newton’s Method (Variable Matrix Method)- Continued Given the objective function f(x) a bx 1/2xTHx, then f b Hx, and fk 1- f k H(xk 1- xk ), or xk 1- xk H-1 gk where gk fk 1- f k Let Ak 1 H-1 Ak Ak xk 1- xk (Ak Ak ) gk Ak gk xk- Ak gk Finally, A x y A g z T k k y T g k T k k z T g k
Quasi-Newton’s Method – Continued Choose y xk, z Ak gk (The Davidon-Flecher-Powell’s method Broyden-Flecher-Shanno’s Method Summary: A ( k 1) x ( k ) g ( k )T k x ( k ) g ( k )T x ( k ) x ( k )T I A I ( k )T ( k ) ( k )T (k ) ( k )T (k ) x g x g x g In the first run, given initial conditions and convergence criteria, and evaluate the gradient First direction is on the negative of the gradient, Ak I In the iteration phase, evaluate the new gradient and find gk, xk, and solve Ak using the equation in the previous slide The new direction is on sk 1 Ak 1 f k 1 Check convergence, and continue the iteration phase
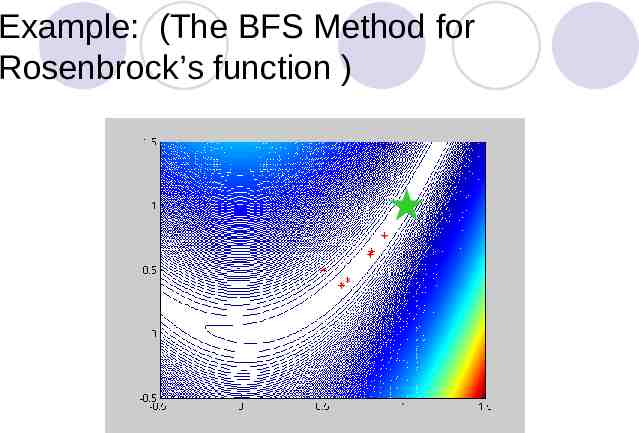
Example: (The BFS Method for Rosenbrock’s function )
Heuristic Approaches (1) s-2 Simplex Approach Main Idea Trial Point Base Point Rules 1: Straddled: Selected the “worse” vertex generated in the previous iteration, then choose instead the vertex with the next highest function value 2. Cycling: In a given vertex unchanged more than M iterations, reduce the size by some factor 3. Termination: The search is terminated when the simlex gets small enough.
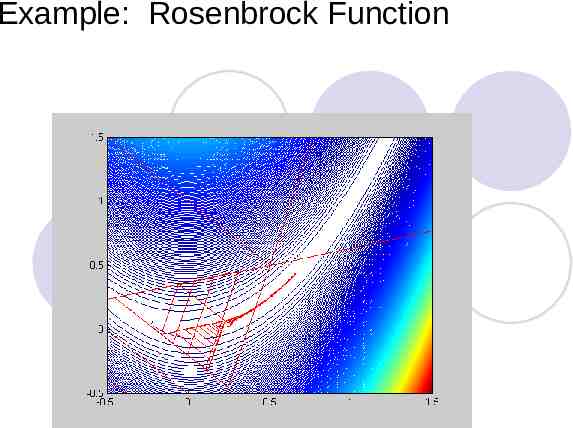
Example: Rosenbrock Function
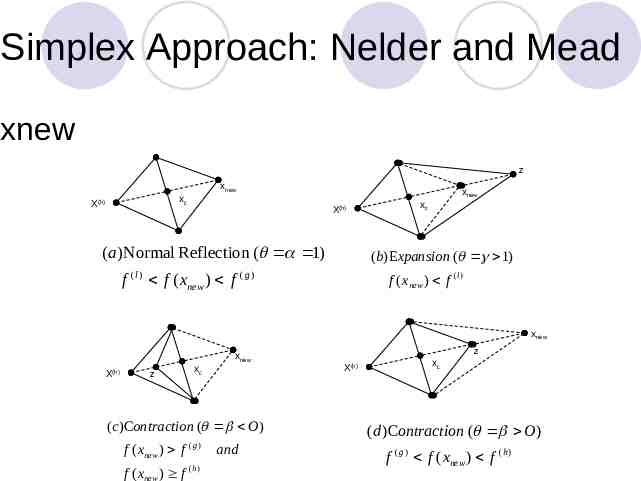
Simplex Approach: Nelder and Mead xnew z xnew xc X(h) xnew xc X (h) (a) Normal Reflection ( 1) (b) Expansion ( 1) f (l ) f ( xnew ) f ( g ) f ( xnew ) f (l ) xnew xnew X(h) z xc (c)Contraction ( O) f ( xnew ) f (g) f ( xnew ) f ( h ) z X (h) and xc (d )Contraction ( O) f ( g ) f ( xnew ) f ( h )
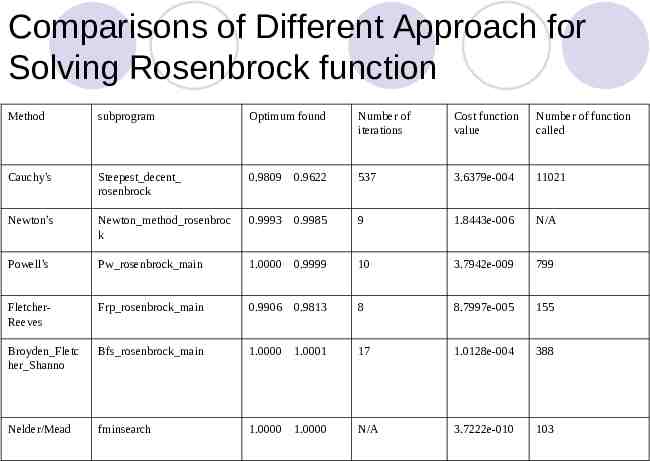
Comparisons of Different Approach for Solving Rosenbrock function Method subprogram Optimum found Number of iterations Cost function value Number of function called Cauchy’s Steepest decent rosenbrock 0.9809 0.9622 537 3.6379e-004 11021 Newton’s Newton method rosenbroc k 0.9993 0.9985 9 1.8443e-006 N/A Powell’s Pw rosenbrock main 1.0000 0.9999 10 3.7942e-009 799 FletcherReeves Frp rosenbrock main 0.9906 0.9813 8 8.7997e-005 155 Broyden Fletc her Shanno Bfs rosenbrock main 1.0000 1.0001 17 1.0128e-004 388 Nelder/Mead fminsearch 1.0000 1.0000 N/A 3.7222e-010 103
Heuristic Approach (Reduction Sampling with Random Search) Step 1: Given initial sampling radius and initial center of the generate a random N points within the region. Step 2: Get the best of the N sampling as the new center of the circle. Step 3: Reduce the radius of the search circle, if the radius is not small enough, go back to step 2, otherwise stop.