Chapter 3 Mathematics of Finance Section 3 Future Value of an Annuity;

Chapter 3 Mathematics of Finance Section 3 Future Value of an Annuity; Sinking Funds

Learning Objectives for Section 3.3 Future Value of an Annuity: Sinking Funds The student will be able to compute the future value of an annuity. The student will be able to solve problems involving sinking funds. The student will be able to approximate interest rates of annuities. Barnett/Ziegler/Byleen Finite Mathematics 12e 2

Definition of Annuity An annuity is any sequence of equal periodic payments. An ordinary annuity is one in which payments are made at the end of each time interval. If for example, 100 is deposited into an account every quarter (3 months) at an interest rate of 8% per year, the following sequence illustrates the growth of money in the account after one year: 0.08 100 100 1 100 (1.02 )(1.02) 100(1.02)(1.02)(1.02) 4 100 100(1.02) 100(1.02) 2 100(1.02)3 3rd qtr 2nd quarter 1st quarter This amount was just put in at the end of the 4th quarter, so it has earned no interest. Barnett/Ziegler/Byleen Finite Mathematics 12e 3

General Formula for Future Value of an Annuity n (1 i) 1 FV PMT i where FV future value (amount) PMT periodic payment i rate per period n number of payments (periods) Note: Payments are made at the end of each period. Barnett/Ziegler/Byleen Finite Mathematics 12e 4

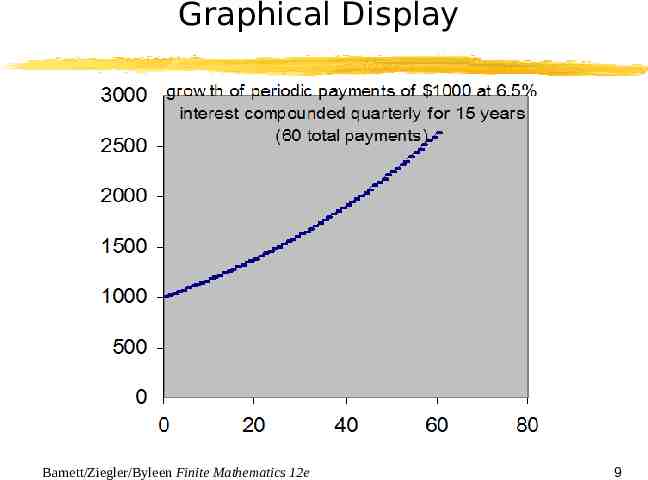
Example Suppose a 1000 payment is made at the end of each quarter and the money in the account is compounded quarterly at 6.5% interest for 15 years. How much is in the account after the 15 year period? Barnett/Ziegler/Byleen Finite Mathematics 12e 5

Example Suppose a 1000 payment is made at the end of each quarter and the money in the account is compounded quarterly at 6.5% interest for 15 years. How much is in the account after the 15 year period? (1 i ) n 1 Solution: FV PMT i 0.065 4(15) 1 1 4 100,336.68 FV 1000 0.065 4 Barnett/Ziegler/Byleen Finite Mathematics 12e 6

Amount of Interest Earned How much interest was earned over the 15 year period? Barnett/Ziegler/Byleen Finite Mathematics 12e 7

Amount of Interest Earned Solution How much interest was earned over the 15 year period? Solution: Each periodic payment was 1000. Over 15 years, 15(4) 60 payments were made for a total of 60,000. Total amount in account after 15 years is 100,336.68. Therefore, amount of accrued interest is 100,336.68 60,000 40,336.68. Barnett/Ziegler/Byleen Finite Mathematics 12e 8

Graphical Display Barnett/Ziegler/Byleen Finite Mathematics 12e 9

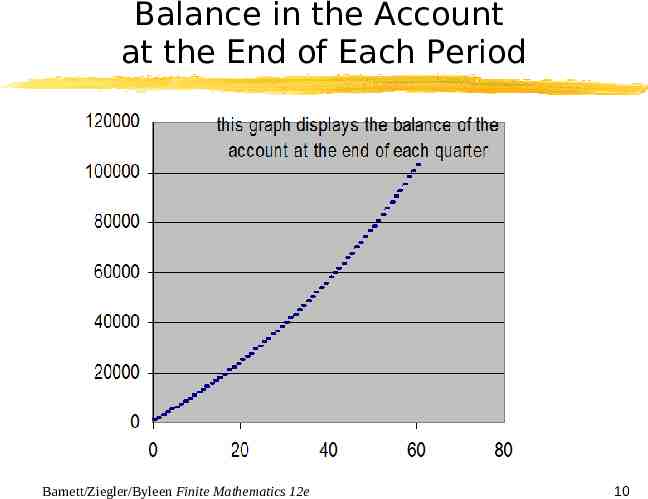
Balance in the Account at the End of Each Period Barnett/Ziegler/Byleen Finite Mathematics 12e 10

Sinking Fund Definition: Any account that is established for accumulating funds to meet future obligations or debts is called a sinking fund. The sinking fund payment is defined to be the amount that must be deposited into an account periodically to have a given future amount. Barnett/Ziegler/Byleen Finite Mathematics 12e 11

Sinking Fund Payment Formula To derive the sinking fund payment formula, we use algebraic techniques to rewrite the formula for the future value of an annuity and solve for the variable PMT: (1 i)n 1 FV PMT i i FV PMT n (1 i ) 1 Barnett/Ziegler/Byleen Finite Mathematics 12e 12

Sinking Fund Sample Problem How much must Harry save each month in order to buy a new car for 12,000 in three years if the interest rate is 6% compounded monthly? Barnett/Ziegler/Byleen Finite Mathematics 12e 13

Sinking Fund Sample Problem Solution How much must Harry save each month in order to buy a new car for 12,000 in three years if the interest rate is 6% compounded monthly? Solution: i FV PMT n (1 i ) 1 0.06 12 pmt 305.06 12000 0.06 36 1 1 12 Barnett/Ziegler/Byleen Finite Mathematics 12e 14

Approximating Interest Rates Example Mr. Ray has deposited 150 per month into an ordinary annuity. After 14 years, the annuity is worth 85,000. What annual rate compounded monthly has this annuity earned during the 14 year period? Barnett/Ziegler/Byleen Finite Mathematics 12e 15

Approximating Interest Rates Solution Mr. Ray has deposited 150 per month into an ordinary annuity. After 14 years, the annuity is worth 85,000. What annual rate compounded monthly has this annuity earned during the 14 year period? Solution: Use the FV formula: Here FV 85,000, PMT 150 and n, the number of payments is 14(12) 168. Substitute these values into the formula. Solution is approximated graphically. Barnett/Ziegler/Byleen Finite Mathematics 12e 16

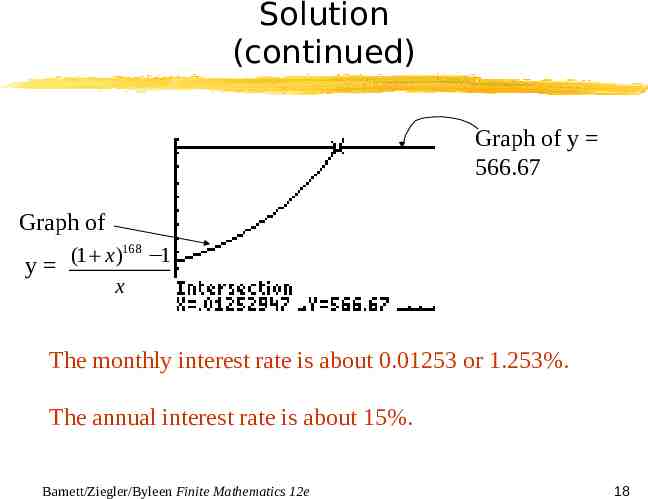
Solution (continued) (1 i ) n 1 FV PMT i (1 i )14(12) 1 85,000 150 i Graph each side of the last equation separately on a graphing calculator and find the point of intersection. 85,000 (1 i )168 1 150 i (1 x)168 1 85, 000 y 566.67 x 150 Barnett/Ziegler/Byleen Finite Mathematics 12e 17

Solution (continued) Graph of y 566.67 Graph of (1 x)168 1 y x The monthly interest rate is about 0.01253 or 1.253%. The annual interest rate is about 15%. Barnett/Ziegler/Byleen Finite Mathematics 12e 18