Chapter 12 Solutions 8–1 John A. Schreifels Chemistry 212 Chapter 12-1

Chapter 12 Solutions 8–1 John A. Schreifels Chemistry 212 Chapter 12-1

Overview Solution formation – Types of solution – Solubility and the solution process – Effect of temperature and pressure on solubility Colligative properties – – – – – Ways of expressing concentration Vapor pressure of a solution Boiling-point elevation and freezing point depression. Osmosis Colligative properties of ionic solutions Colloid Formation – Colloids John A. Schreifels Chemistry 212 8–2 Chapter 12-2

Types of Solution Solution – homogeneous mixture of two or more substances of ions or molecules. E.g. NaCl (aq) – Solvent component which is the component in greater amount. – Solute component which is present in the smaller amount. – Gaseous gases are completely miscible in each other. – Liquid gas, liquid or solid solute dissolved in solute. – Solid mixture of two solids that are miscible in each other to form a single phase. Colloid – appears to be a homogeneous mixture, but particles are much bigger, but not filterable. E.g. Fog, smoke, whipped cream, mayonnaise, etc. Suspension: larger particle sizes, filterable. E.g. mud, freshly squeezed orange juice. John A. Schreifels Chemistry 212 Chapter 12-3 8–3

Solubility and the Solution Process The solid dissolves rapidly at first but as the solution approaches saturation the net rate of dissolution decreases since the process is in dynamic equilibrium. When the solution has reached equilibrium the amount of solute does not change with time; At equilibrium: the rate of dissolution rate of solution Fig. 12.2 Solubility Equilibrium 8–4 John A. Schreifels Chemistry 212 Chapter 12-4

Solubility and the Solution Process II Saturated solution: maximum amount of solute is dissolved in solvent. Trying to dissolve more results in undissolved solute in container. Solubility: Amount of solute that dissolves in a solvent to produce a saturated solution. (Solubility often expressed in g/100 mL.) E.g. 0.30 g of I2 dissolved in 1000 g of H2O. Unsaturated solution: less than max. amount of solute is dissolved in solvent. E.g. 0.20 g of I2 dissolved in 1000 g of H2O. Supersaturation more solute in solution than normally allowed; we call this a supersaturated solution. John A. Schreifels Chemistry 212 Chapter 12-5 8–5

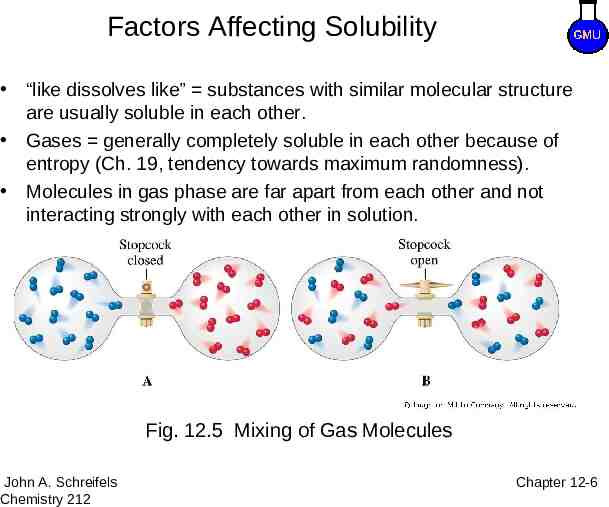
Factors Affecting Solubility “like dissolves like” substances with similar molecular structure are usually soluble in each other. Gases generally completely soluble in each other because of entropy (Ch. 19, tendency towards maximum randomness). Molecules in gas phase are far apart from each other and not interacting strongly with each other in solution. 8–6 Fig. 12.5 Mixing of Gas Molecules John A. Schreifels Chemistry 212 Chapter 12-6

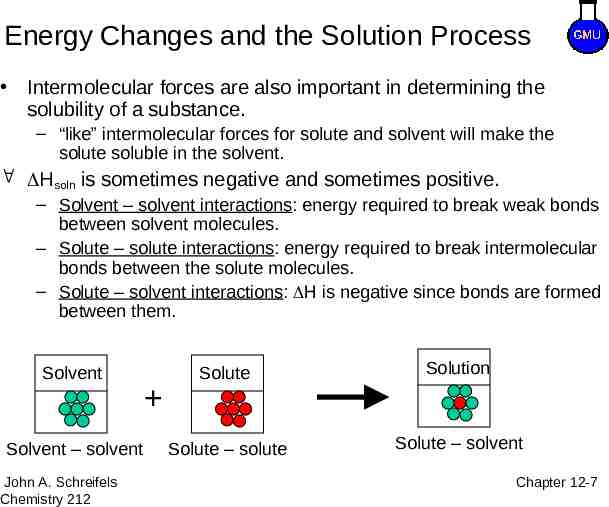
Energy Changes and the Solution Process Intermolecular forces are also important in determining the solubility of a substance. – “like” intermolecular forces for solute and solvent will make the solute soluble in the solvent. Hsoln is sometimes negative and sometimes positive. – Solvent – solvent interactions: energy required to break weak bonds between solvent molecules. – Solute – solute interactions: energy required to break intermolecular bonds between the solute molecules. – Solute – solvent interactions: H is negative since bonds are formed between them. Solvent Solvent – solvent John A. Schreifels Chemistry 212 Solute Solution 8–7 Solute – solute Solute – solvent Chapter 12-7

Molecular Solutions Molecular compounds with similar chemical structures and polarities tend to be miscible. Homologous alcohol series have polar and non-polar ends. 8–8 John A. Schreifels Chemistry 212 Chapter 12-8

Ionic Solutions Solubility affected by: – Energy of attraction (due Ion-dipole force) affects the solubility. Also called hydration energy, – Lattice energy (energy holding the ions together in the lattice. Related to the charge on ions; larger charge means higher lattice energy. Inversely proportional to the size of the ion; large ions mean smaller lattice energy. Solubility increases with increasing ion size, due to decreasing lattice energy; Mg(OH)2(least soluble), Ca(OH)2, Sr(OH)2, Ba(OH)2(most soluble) (lattice energy changes dominant). Energy of hydration increases with for smaller ions than bigger ones; thus ion size. MgSO4(most soluble),. BaSO4 (least soluble.) Hydration energy dominant. John A. Schreifels Chemistry 212 Chapter 12-9 8–9

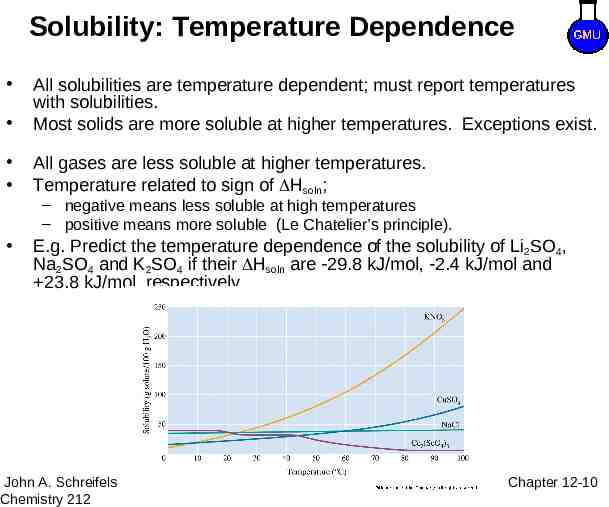
Solubility: Temperature Dependence All solubilities are temperature dependent; must report temperatures with solubilities. Most solids are more soluble at higher temperatures. Exceptions exist. All gases are less soluble at higher temperatures. Temperature related to sign of Hsoln; – negative means less soluble at high temperatures – positive means more soluble (Le Chatelier’s principle). E.g. Predict the temperature dependence of the solubility of Li2SO4, Na2SO4 and K2SO4 if their Hsoln are 29.8 kJ/mol, 2.4 kJ/mol and 23.8 kJ/mol, respectively. 8–10 John A. Schreifels Chemistry 212 Chapter 12-10

Solubility: Pressure Dependence Pressure has little effect on the solubility of a liquid or solid, but has dramatic effect on gas solubility in a liquid. Henry’s law S kHP. Allows us to predict the solubility of a gas at any pressure. E.g. At 25 C P(O2 in air) 0.21 atm. Its solubility in water is 3.2x10 4M. Determine its solubility when pressure of O2 1.00 atm. 8–11 John A. Schreifels Chemistry 212 Chapter 12-11

Units of Concentration Physical properties of solutions are often related to the concentration of the solute moles of solute Molarity in the solution.Molarity liter of solution Mole fraction: The same quantity we mol of A have used in fractional abundances as X well as with gases (Dalton’s law). A mol A mol B unitless number. mass of solute Weight (mass) Percent (wt%) – similar 2 wt % x 10 to mole fraction except use mass of each. mass of solution E.g. determine the wt% of a solution prepared by dissolving 1.44 g of NaCl in 100.0 mL of water. Assume that the density of water is 1.00 g/mL mass of solute Other units: parts per million (ppm) and 6 ppm x 10 parts per billion (ppb) for small mass of solution concentrations. 8–12 ppb John A. Schreifels Chemistry 212 mass of solute x10 9 mass of solution Chapter 12-12

Units of Concentration2 Molality(m): defined as the mol of solute per kg of solvent. Unlike Molarity this unit is temperature independent. mol solute Molality (m) mass of solvent (kg) E.g. determine the molality of a solution prepared by dissolving 1.44 g NaCl into exactly 100.0 mL of water. Assume the density of water is 1.00 g/mL. E.g.2 Determine mass % of solution made from dissolving 30.0 g H2O2 with 70.0 g H2O. E.g.3 Determine molality of 30% H2O2(aq) E.g.4 Determine the mole fraction of the compound in E.g. 3 E.g.5 Concentrated ammonia is 14.8 M and has a density of 8–13 0.900 g/mL. What is the molar volume and the molality? John A. Schreifels Chemistry 212 Chapter 12-13

Physical Behavior of Solutions: Colligative Properties Compared with the pure solvent the solution’s: – – – – Vapor pressure is lower Boiling point is elevated Freezing point is lower Osmosis occurs from solvent to solution when separated by a membrane. 8–14 John A. Schreifels Chemistry 212 Chapter 12-14

Vapor-Pressure Lowering of Solutions: Raoult’s Law Raoult’s Law: Psoln PsolvxXsolv Non–volatile solute: vapor pressure decreases upon addition of solute. Linear for dilute solutions Vapor pressure lowering : P Po P Po(1 Xsolv) E.g. Determine vapor pressure lowering when 5.00 g of sucrose added to 100.0 g of H2O. FM(sucrose) 342.3 g/mol. The vapor pressure of water at 25 C is 23.8 mmHg. E.g. 2 Determine the mass of sucrose dissolved in 100.0 g of water if the vapor pressure was 20.0 mmHg. 8–15 John A. Schreifels Chemistry 212 Chapter 12-15

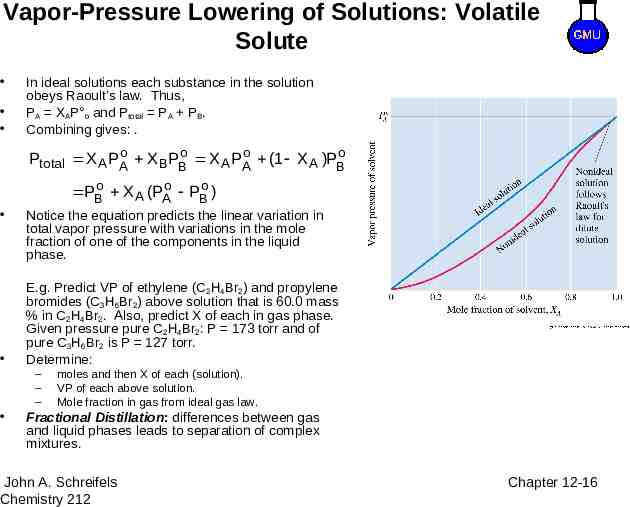
Vapor-Pressure Lowering of Solutions: Volatile Solute In ideal solutions each substance in the solution obeys Raoult’s law. Thus, PA XAP o and Ptotal PA PB. Combining gives: . Ptotal X A PAo X BPBo X A PAo (1 X A )PBo PBo X A (PAo PBo ) Notice the equation predicts the linear variation in total vapor pressure with variations in the mole fraction of one of the components in the liquid phase. E.g. Predict VP of ethylene (C2H4Br2) and propylene bromides (C3H6Br2) above solution that is 60.0 mass % in C2H4Br2. Also, predict X of each in gas phase. Given pressure pure C2H4Br2: P 173 torr and of pure C3H6Br2 is P 127 torr. Determine: – – – moles and then X of each (solution). VP of each above solution. Mole fraction in gas from ideal gas law. Fractional Distillation: differences between gas and liquid phases leads to separation of complex mixtures. John A. Schreifels Chemistry 212 8–16 Chapter 12-16

BP Elevation and FP Depression of Solutions The magnitude of the change in FP and BP is directly proportional to the concentration of the solute (molality) – expressed in terms of the total number of particles in the solution. BP Elevation The magnitude of the BP increase is given by the equation: Tb K b m where Kb has units of Ckg/mol or C/m FP Depression: linear variation with composition and given by: Tf K f m where the units for this constant are the same as for K b E.g. Determine freezing point depression when 5.00 g of sucrose is added to 100.0 g of H2O. FM(sucrose) 342.3 g/mol. Kf 1.86 C/m. E.g. Determine the BP elevation for the sucrose solution in the previous example. Kb 0.521 C/m. John A. Schreifels Chemistry 212 8–17 Chapter 12-17

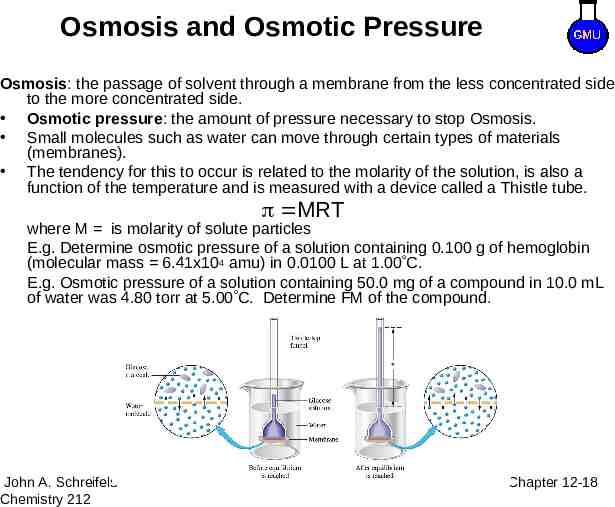
Osmosis and Osmotic Pressure Osmosis: the passage of solvent through a membrane from the less concentrated side to the more concentrated side. Osmotic pressure: the amount of pressure necessary to stop Osmosis. Small molecules such as water can move through certain types of materials (membranes). The tendency for this to occur is related to the molarity of the solution, is also a function of the temperature and is measured with a device called a Thistle tube. MRT where M is molarity of solute particles E.g. Determine osmotic pressure of a solution containing 0.100 g of hemoglobin (molecular mass 6.41x104 amu) in 0.0100 L at 1.00 C. E.g. Osmotic pressure of a solution containing 50.0 mg of a compound in 10.0 mL of water was 4.80 torr at 5.00 C. Determine FM of the compound. 8–18 John A. Schreifels Chemistry 212 Chapter 12-18

Reverse Osmosis Application of a pressure to the solution (that is equal to or greater than the Osmotic pressure) and the solvent flows from the more concentrated side to the other one. This process is used to obtain pure water from salt water. 8–19 John A. Schreifels Chemistry 212 Chapter 12-19

Colligative Properties of Ionic Solutions Colligative properties of solutions depends upon the total concentration of particles. Each equation describing colligative properties must be modified to account for this with ionic solutions since each ionic compound gives more than one mole of ions for every mole of compound. – BP elevation: – Freezing point depression: – Osmotic pressure: Where i van’t Hoff factor. Tb K b m i Tf K f m i i M R T van’t Hoff factor can be something other than integer under certain circumstances, but for completely ionic solutions is equal to the number of ions/ionic compound to be found in solution: E.g. NaCl: i 2; Na2SO4: i 3; John A. Schreifels Chemistry 212 8–20 Chapter 12-20