Basic Laws of Electric Cicuits Ohms Law Kirchhoff’s Current Law
21 Slides218.00 KB
Basic Laws of Electric Cicuits Ohms Law Kirchhoff’s Current Law Lesson 2
Basic Laws of Circuits Ohm’s Law: The voltage across a resistor is directly proportional to the current moving through the resistor. i(t) v (t) v (t) R i(t) (2.1) R i(t) v (t) R 1 v (t) R i(t) (2.2)
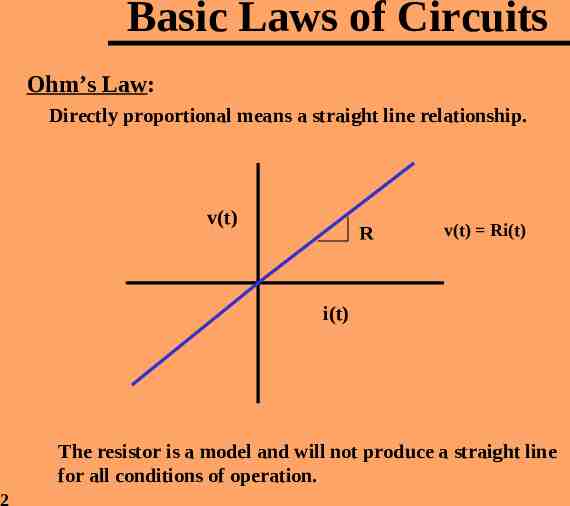
Basic Laws of Circuits Ohm’s Law: Directly proportional means a straight line relationship. v(t) R v(t) Ri(t) i(t) The resistor is a model and will not produce a straight line for all conditions of operation. 2
Basic Laws of Circuits Ohm’s Law: About Resistors: The unit of resistance is ohms( ). A mathematical expression for resistance is l R A l : The length of the conductor (meters ) A : The cross sectional area (meters 2 ) : The resistivity m 3 (2.3)
Basic Laws of Circuits Ohm’s Law: About Resistors: We remember that resistance has units of ohms. The reciprocal of resistance is conductance. At one time, conductance commonly had units of mhos (resistance spelled backwards). In recent years the units of conductance has been established as seimans (S). Thus, we express the relationship between conductance and resistance as 1 G R (S) (2.4) We will see later than when resistors are in parallel, it is convenient to use Equation (2.4) to calculate the equivalent resistance. 4
Basic Laws of Circuits Ohm’s Law: Ohm’s Law: Example 2.1. Consider the following circuit. 115V R M S (a c ) V R (1 0 0 W a tt lig h t b u lb ) Determine the resistance of the 100 Watt bulb. V2 P VI I 2R R V 2 1152 R 132.25 ohms P 100 5 (2.5) A suggested assignment is to measure the resistance of a 100 watt light bulb with an ohmmeter. Debate the two answers.
Basic Laws of Circuits Ohm’s Law: Property of Resistance: Resistivities of some basic materials Material silver copper aluminum gold carbon germanium silicon paper mica glass teflon 6 Resistivity (ohm meters) 1.6x10-8 1.7x10-8 2.8x10-8 2.5x10-8 4.1x10-5 47x10-2 6.4x102 1x1010 5x1011 1x1012 3x1012 Common Use conductor conductor conductor conductor semiconductor semiconductor semiconductor insulator insulator insulator insulator
Basic Laws of Circuits Ohm’s Law: Property of Resistance Why are some materials better conductors than others? Consider copper. v a le n c e e le c tr o n 7 Copper Atom v a le n c e s h e ll
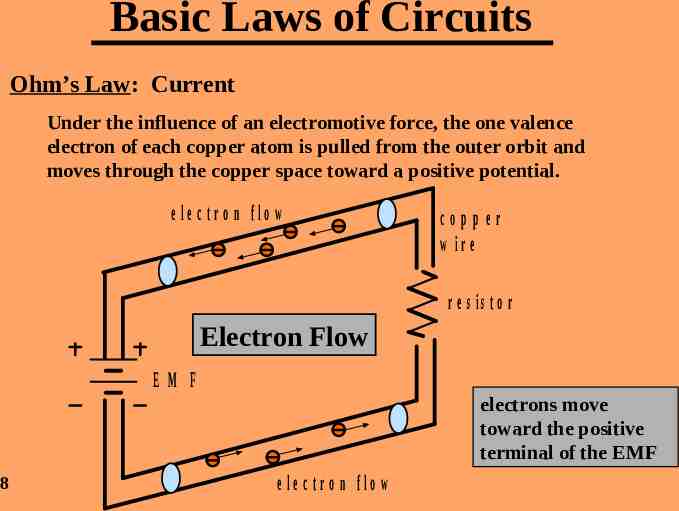
Basic Laws of Circuits Ohm’s Law: Current Under the influence of an electromotive force, the one valence electron of each copper atom is pulled from the outer orbit and moves through the copper space toward a positive potential. e le c tr o n flo w copper w ir e r e s is to r Electron Flow E M F electrons move toward the positive terminal of the EMF 8 e le c t r o n f lo w
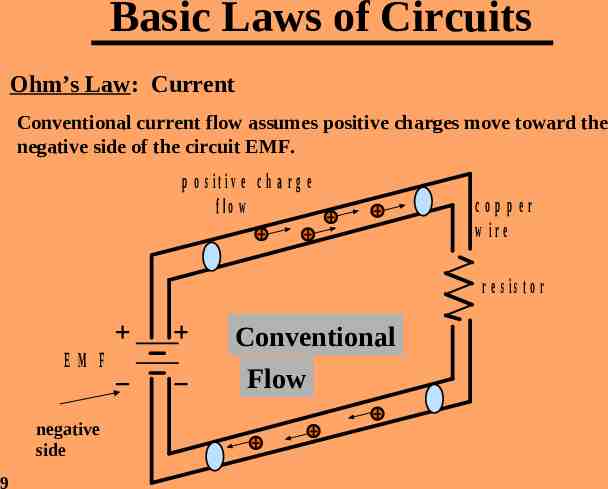
Basic Laws of Circuits Ohm’s Law: Current Conventional current flow assumes positive charges move toward the negative side of the circuit EMF. p o s it iv e c h a r g e flo w copper w ir e r e s is to r E M F negative side 9 Conventional Flow
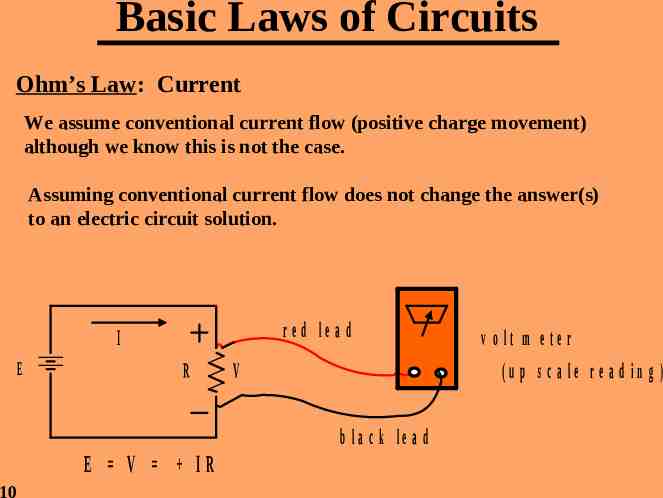
Basic Laws of Circuits Ohm’s Law: Current We assume conventional current flow (positive charge movement) although we know this is not the case. Assuming conventional current flow does not change the answer(s) to an electric circuit solution. r e d le a d I E R V (u p s c a le r e a d in g ) b la c k le a d E V IR 10 v o lt m e te r
Basic Laws of Circuits Kirchhoff’s Current Law As a consequence of the Law of the conservation of charge, we have: The sum of the current entering a node (junction point) equal to the sum of the currents leaving. Ia Id Ic Ib Ia Ib Ic Id I a, I b , I c , a n d I d c a n e a c h b e e ith e r a p o s itiv e o r n e g a tiv e n u m b e r . 11
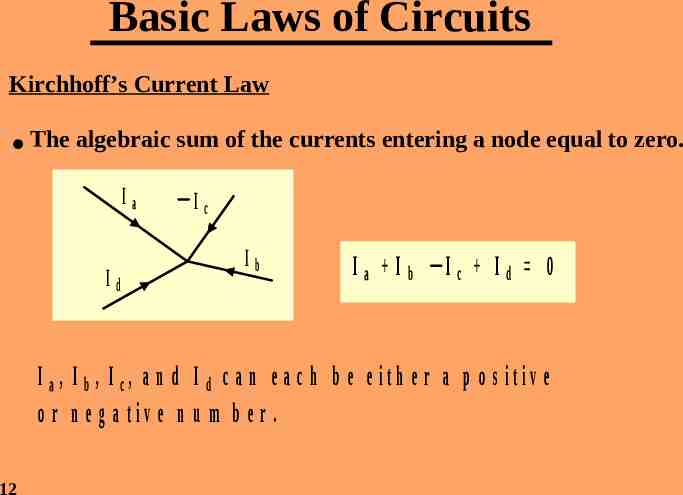
Basic Laws of Circuits Kirchhoff’s Current Law The algebraic sum of the currents entering a node equal to zero. Ia Id Ic Ib Ia Ib Ic Id 0 I a, I b , I c, a n d I d c a n e a c h b e e ith e r a p o s itiv e o r n e g a tiv e n u m b e r . 12
Basic Laws of Circuits Kirchhoff’s Current Law The algebraic sum of the currents leaving a node equal to zero. Ia Id Ic Ib Ia - Ib Ic Id 0 I a, I b , I c, a n d I d c a n e a c h b e e ith e r a p o s itiv e o r n e g a tiv e n u m b e r . 13
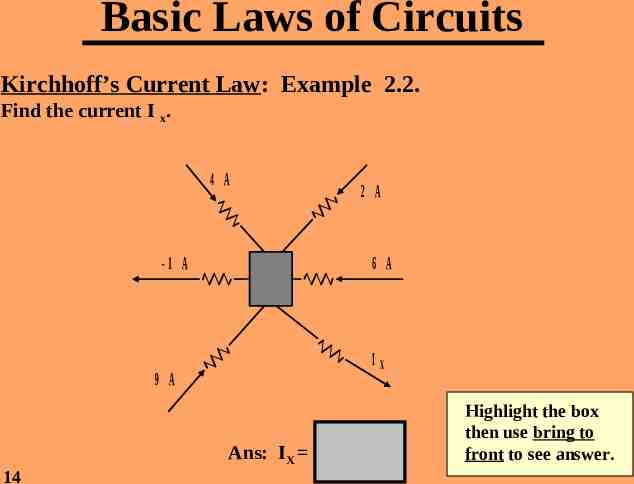
Basic Laws of Circuits Kirchhoff’s Current Law: Example 2.2. Find the current I x. 4 A -1 A 6 A IX 9 A Ans: IX 14 2 A 22 A Highlight the box then use bring to front to see answer.
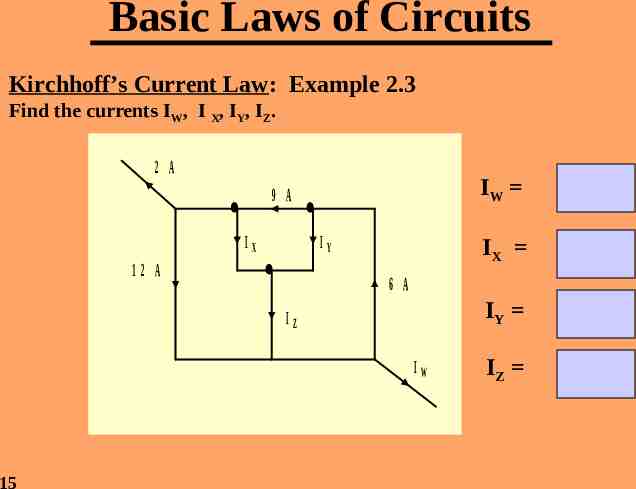
Basic Laws of Circuits Kirchhoff’s Current Law: Example 2.3 Find the currents IW, I X, IY, IZ. 2 A 9 A IX 12 A IY -2 A IX -5 A IY -3 A IZ -8 A 6 A IZ IW 15 IW
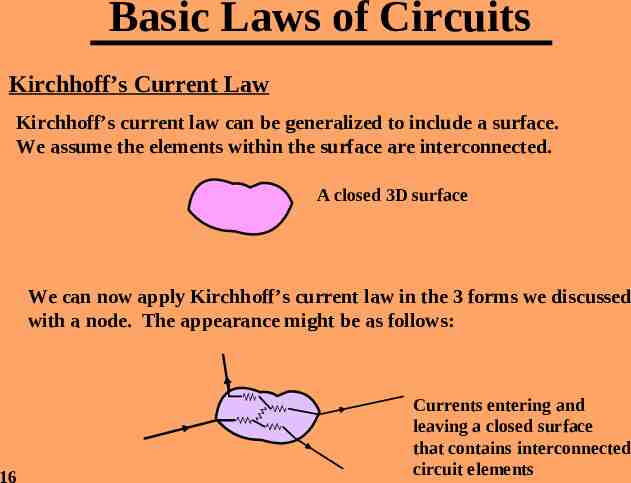
Basic Laws of Circuits Kirchhoff’s Current Law Kirchhoff’s current law can be generalized to include a surface. We assume the elements within the surface are interconnected. A closed 3D surface We can now apply Kirchhoff’s current law in the 3 forms we discussed with a node. The appearance might be as follows: 16 Currents entering and leaving a closed surface that contains interconnected circuit elements
Basic Laws of Circuits Kirchhoff’s Current Law As a consequence of the Law of the conservation of charge, we have: j N C ir c u it k M i j ik j 1 k 1 r Q C ir c u it ir r 1 0 m Q C ir c u it 17 im m 1 0
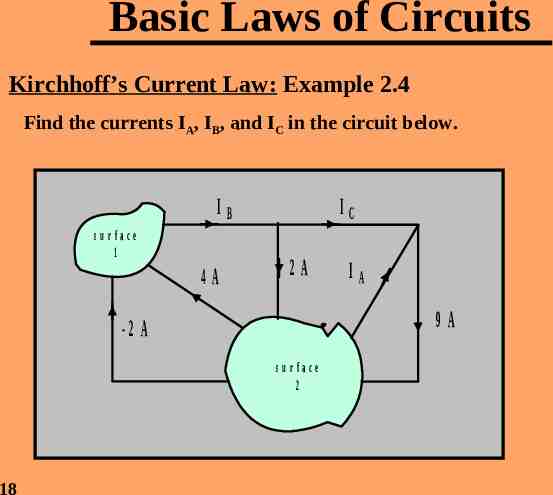
Basic Laws of Circuits Kirchhoff’s Current Law: Example 2.4 Find the currents IA, IB, and IC in the circuit below. IB su rfa ce 1 4A IC 2A 9A -2 A su rfa ce 2 18 IA
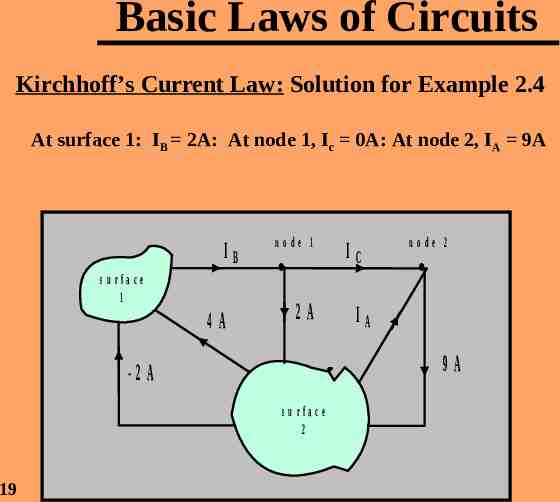
Basic Laws of Circuits Kirchhoff’s Current Law: Solution for Example 2.4 At surface 1: IB 2A: At node 1, Ic 0A: At node 2, IA 9A IB su rfa ce 1 4A node 1 2A node 2 IA 9A -2 A su rfa ce 2 19 IC
Basic Electric Circuit Concepts circuits End of Lesson 2 Ohm’s Law Kirchhoff’s Current Law