AP Physics 1 – Unit 2 DYNAMICS OF FORCE AND MOTION

AP Physics 1 – Unit 2 DYNAMICS OF FORCE AND MOTION

Newton’s Laws

Learning Objectives: BIG IDEA 1: Objects and systems have properties such as mass and charge. Systems may have internal structure.1.C.1.1: I can design an experiment for collecting data to determine the relationship between the net force exerted on an object its inertial mass and its acceleration. [SP 4.2] 1.C.3.1: I can design a plan for collecting data to measure gravitational mass and to measure inertial mass and to distinguish between the two experiments. [SP 4.2] BIG IDEA 2: Fields existing in space can be used to explain interactions. 2.B.1.1: I can calculate the gravitational force on an object with mass m in a gravitational field of strength g in the context of the effects of a net force on objects and systems. [SP 2.2, 7.2]

Learning Objectives BIG IDEA 3: The interactions of an object with other objects can be described by forces. 3.A.2.1: I can represent forces in diagrams or mathematically using appropriately labeled vectors with magnitude, direction, and units during the analysis of a situation. [SP 1.1] 3.A.3.1: I can analyze a scenario and make claims (develop arguments, justify assertions) about the forces exerted on an object by other objects for different types of forces or components of forces. [SP 6.4, 7.2] 3.A.3.2: I can challenge a claim that an object can exert a force on itself. [SP 6.1] 3.A.3.3: I can describe a force as an interaction between two objects and identify both objects for any force. [SP 1.4] 3.A.4.1: I can construct explanations of physical situations involving the interaction of bodies using Newton’s third law and the representation of action-reaction pairs of forces. [SP 1.4, 6.2] 3.A.4.2: I can use Newton’s third law to make claims and predictions about the action-reaction pairs of forces when two objects interact. [SP 6.4, 7.2] 3.B.1.1: I can predict the motion of an object subject to forces exerted by several objects using an application of Newton’s second law in a variety of physical situations with acceleration in one dimension. [SP 6.4, 7.2]

Learning Objectives 3.B.1.2: I can design a plan to collect and analyze data for motion (static, constant, or accelerating) from force measurements and carry out an analysis to determine the relationship between the net force and the vector sum of the individual forces. [SP 4.2, 5.1] 3.B.1.3: I can reexpress a free-body diagram representation into a mathematical representation and solve the mathematical representation for the acceleration of the object. [SP 1.5, 2.2] 3.B.2.1: I can create and use free-body diagrams to analyze physical situations to solve problems with motion qualitatively and quantitatively. [SP 1.1, 1.4, 2.2] 3.C.4.1: I can make claims about various contact forces between objects based on the microscopic cause of those forces. [SP 6.1] 3.C.4.2: I can explain contact forces (tension, friction, normal, spring) as arising from interatomic electric forces and that they therefore have certain directions. [SP 6.2]

Learning Objectives BIG IDEA 4: Interactions between systems can result in changes in those systems. 4.A.1.1: I can use representations of the center of mass of an isolated two-object system to analyze the motion of the system qualitatively and semi-quantitatively. [SP 1.2, 1.4, 2.3, 6.4] 4.A.2.1: I can make predictions about the motion of a system based on the fact that acceleration is equal to the change in velocity per unit time, and velocity is equal to the change in position per unit time. [SP 6.4] 4.A.2.2: I can evaluate using given data whether all the forces on a system or whether all the parts of a system have been identified. [SP 5.3] 4.A.2.3: I can create mathematical models and analyze graphical relationships for acceleration, velocity, and position of the center of mass of a system and use them to calculate properties of the motion of the center of mass of a system. [SP 1.4, 2.2] 4.A.3.1: I can apply Newton’s second law to systems to calculate the change in the center-of-mass velocity when an external force is exerted on the system. [SP 2.2] 4.A.3.2: I can use visual or mathematical representations of the forces between objects in a system to predict whether or not there will be a change in the center-of-mass velocity of that system. [SP 1.4]

Force Unit is the NEWTON(N) Is by definition a push or a pull Can exist during physical contact(Tension, Friction, Applied Force) Can exist with NO physical contact, called FIELD FORCES ( gravitational, electric, etc)

1st Law of Motion - Inertia INERTIA – a quantity of matter, also called MASS. Italian for “LAZY”. Unit for MASS kilogram. Weight or Force due to Gravity is how your MASS is effected by gravity. W mg NOTE: MASS and WEIGHT are NOT the same thing. MASS never changes When an object moves to a different planet. What is the weight of an 85.3-kg person on earth? On Mars 3.2 m/s/s)? W mg W (85.3)(9.8) 835.94 N WMARS (85.3)(3.2) 272.96 N

1st Law of Motion - Inertia An object in motion remains in motion in a straight line and at a constant speed OR an object at rest remains at rest, UNLESS acted upon by an EXTERNAL (unbalanced) Force. There are TWO conditions here and one constraint. Condition #1 – The object CAN move but must be at a CONSTANT SPEED Condition #2 – The object is at REST Constraint – As long as the forces are BALANCED!!!!! And if all the forces are balanced the SUM of all the forces is ZERO. The bottom line: There is NO ACCELERATION in this case AND the object must be at EQILIBRIUM ( All the forces cancel out). acc 0 F 0

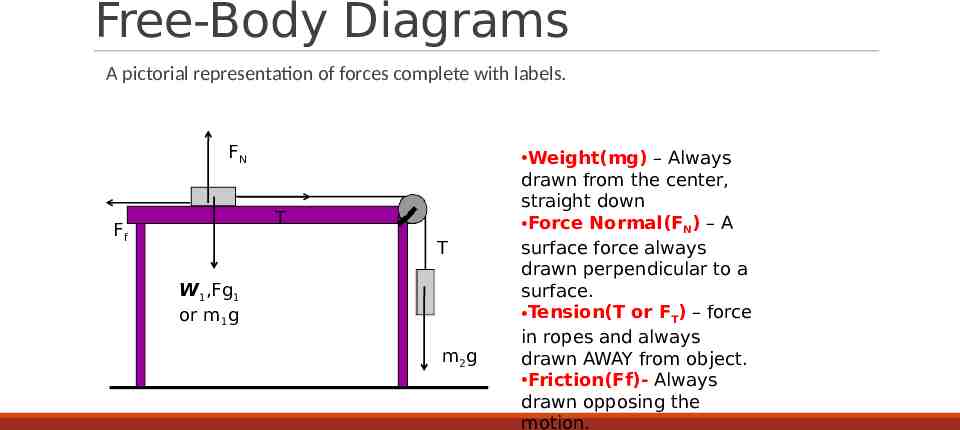
Free-Body Diagrams A pictorial representation of forces complete with labels. FN T Ff T W1,Fg1 or m1g m2g Weight(mg) – Always drawn from the center, straight down Force Normal(FN) – A surface force always drawn perpendicular to a surface. Tension(T or FT) – force in ropes and always drawn AWAY from object. Friction(Ff)- Always drawn opposing the motion.

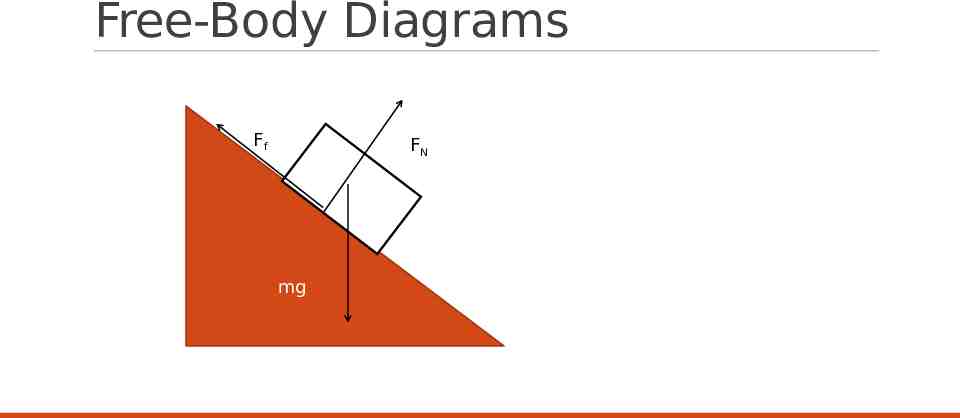
Free-Body Diagrams Ff FN mg

Newton’s 1st Law and Equilibrium Since the Fnet 0, a system moving at a constant speed or at rest MUST be at EQUILIBRIUM. TIPS for solving problems Draw a FBD Resolve anything into COMPONENTS Write equations of equilibrium Solve for unknowns

Example: A 10-kg box is being pulled across the table to the right at a constant speed with a force of 50N. a)Calculate the Force of Friction b)Calculate the Force Normal FN Ff mg Fa Fa F f 50 N mg Fn (10)(9.8) 98N

Example: Suppose the same box is now pulled at an angle of 30 degrees above the horizontal. a)Calculate the Force of Friction Fax Fa cos 50 cos 30 43.3 N b)Calculate the Force Normal F f Fax 43.3 N FN Fa Fay 30 Ff Fax mg FN mg! FN Fay mg FN mg Fay (10)(9.8) 50 sin 30 FN 73N

What if it isn’t at equilibrium? If an object is NOT at rest or moving at a constant speed, that means the FORCES are UNBALANCED. One force(s) in a certain direction over power the others. THE OBJECT WILL THEN ACCELERATE.

Newton’s 2nd Law The acceleration of an object is directly proportional to the NET FORCE and inversely proportional to the mass. a FNET 1 a m FNET a FNET ma m FNET F Tips: Draw an FBD Resolve vectors into components Write equations of motion by adding and subtracting vectors to find the NET FORCE. Always write larger force – smaller force. Solve for any unknowns

Newton’s 2nd Law A 10-kg box is being pulled across the table to the right by a rope with an applied force of 50N. Calculate the acceleration of the box if a 12 N frictional force acts upon it. FN Ff mg Fa In which direction, is this object accelerating? FNet ma The X direction! 50 12 10a So N.S.L. is worked out using the forces in the “x” direction only Fa F f ma a 3.8 m / s 2

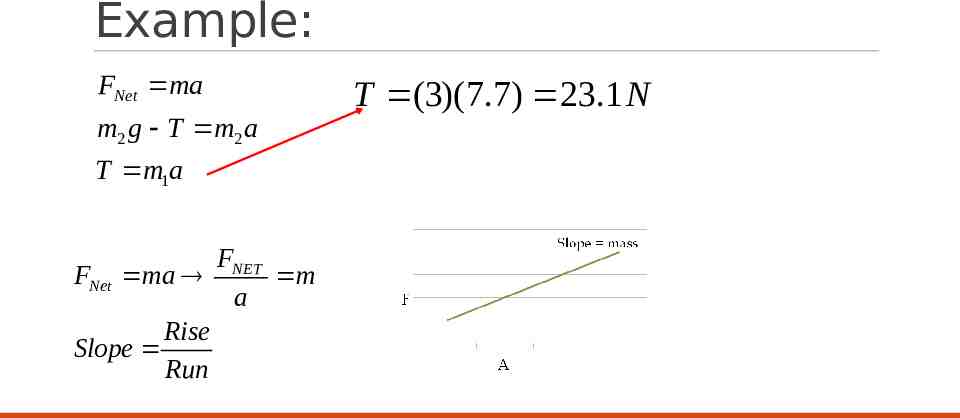
Example: A mass, m1 3.00kg, is resting on a frictionless horizontal table is connected to a cable that passes over a pulley and then is fastened to a hanging mass, m2 11.0 kg as shown below. Find the acceleration of each mass and the tension in the cable. FNet ma FN m2 g T m2 a T m1a T m2 g m1a m2 a m2 g m2 a m1a m2 g a(m2 m1 ) a m2 g (11)(9.8) 7.7 m / s 2 m1 m2 14

Example: FNet ma m2 g T m2 a T m1a FNET FNet ma m a Rise Slope Run T (3)(7.7) 23.1 N

Newton’s 3rd Law “For every action there is an EQUAL and OPPOSITE reaction. This law focuses on action/reaction pairs (forces) They NEVER cancel out All you do is SWITCH the wording! PERSON on WALL WALL on PERSON

Newton’s 3rd Law This figure shows the force during a collision between a truck and a train. You can clearly see the forces are EQUAL and OPPOSITE. To help you understand the law better, look at this situation from the point of view of Newton’s Second Law. FTruck FTrain mTruck ATruck M Train aTrain There is a balance between the mass and acceleration. One object usually has a LARGE MASS and a SMALL ACCELERATION, while the other has a SMALL MASS (comparatively) and a LARGE ACCELERATION.

Examples: Action: HAMMER HITS NAIL Reaction: NAIL HITS HAMMER Action: Earth pulls on YOU Reaction: YOU pull on the earth

Friction KINETIC AND STATIC

Learning Objectives:

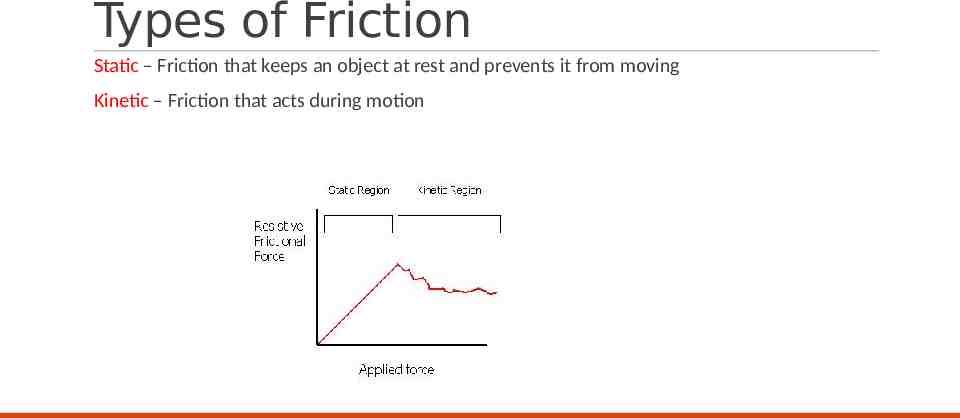
Types of Friction Static – Friction that keeps an object at rest and prevents it from moving Kinetic – Friction that acts during motion

Force of Friction F f FN The Force of Friction is directly related to the Force constant of proportionality Normal. coefficient of friction Mostly due to the fact that BOTH are surface forces Fsf s FN The coefficient of Fkf k FN friction is a unitless constant that is specific to the material type and usually less than one. Note: Friction ONLY depends on the MATERIALS sliding against each other, NOT on surface area.

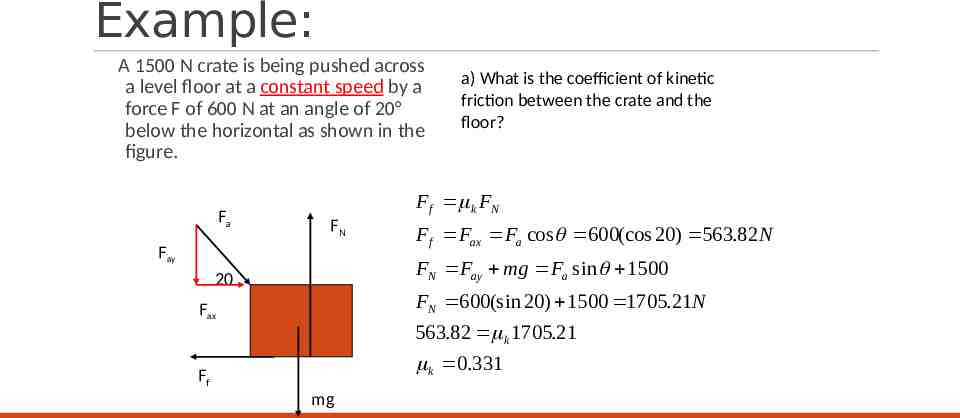
Example: A 1500 N crate is being pushed across a level floor at a constant speed by a force F of 600 N at an angle of 20 below the horizontal as shown in the figure. Fa a) What is the coefficient of kinetic friction between the crate and the floor? F f k FN FN Fay F f Fax Fa cos 600(cos 20) 563.82 N FN Fay mg Fa sin 1500 20 FN 600(sin 20) 1500 1705.21N Fax 563.82 k 1705.21 k 0.331 Ff mg

Example: If the 600 N force is instead pulling the block at an angle of 20 above the horizontal as shown in the figure, what will be the acceleration of the crate. Assume that the coefficient of friction is the same as found in (a) FN 20 Fax FNet ma Fax F f ma Fa cos FN ma Fa cos (mg Fa sin ) ma 600 cos 20 0.331(1500 600 sin 20) 153.1a 563.8 428.57 153.1a a 0.883 m / s 2 Fa 𝐹𝑓 mg Fay

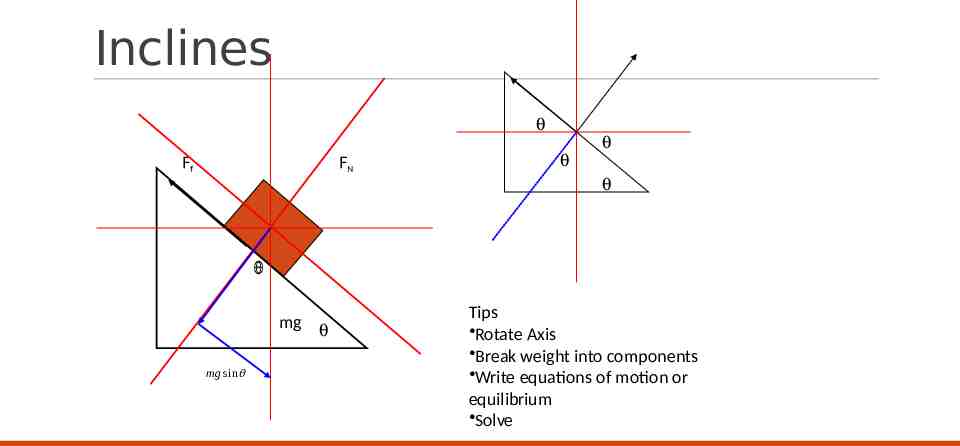
Inclines q Ff FN q q q q mg q mg sin Tips Rotate Axis Break weight into components Write equations of motion or equilibrium Solve

Example: Masses m1 4.00 kg and m2 9.00 kg are connected by a light string that passes over a frictionless pulley. As shown in the diagram, m1 is held at rest on the floor and m2 rests on a fixed incline of angle 40 degrees. The masses are released from rest, and m2 slides 1.00 m down the incline in 4 seconds. Determine (a) The acceleration of each mass (b) The coefficient of kinetic friction and (c) the tension in the string. T FN T m1 g m1a T m1a m1 g m 2 Ff m2gcos40 m2 g sin ( F f T ) m2 a 40 T m2g m1 40 m2gsin40 m 1g FNET ma

FNET ma Example: T m1 g m1a T m1a m1 g m2 g sin ( F f T ) m2 a x vox t 1 at 2 2 1 0 1 a (4) 2 2 a 0.125 m / s 2 T 4(.125) 4(9.8) 39.7 N m2 g sin F f T m2 a m2 g sin F f (m1a m1 g ) m2 a m2 g sin k FN m1a m1 g m2 a m2 g sin k m2 g cos m1a m1 g m2 a m2 g sin m1a m1 g m2 a k m2 g cos k m2 g sin m1a m1 g m2 a m2 g cos k 56.7 0.5 39.2 1.125 0.235 67.57

Newton’s Law of Gravitation

Learning Objectives:

Gravity What causes YOU to be pulled down? THE EARTH .or more specifically the EARTH’S MASS. Anything that has MASS has a gravitational pull towards it. Fg Mm What the proportionality above is saying is that for there to be a FORCE DUE TO GRAVITY on something there must be at least 2 masses involved, where one is larger than the other.

Gravity As you move AWAY from the earth, your DISTANCE increases and your FORCE DUE TO GRAVITY decrease. This is a special INVERSE relationship called an Inverse-Square. 1 Fg 2 r The “r” stands for SEPARATION DISTANCE and is the distance between the CENTERS OF MASS of the 2 objects. We us the symbol “r” as it symbolizes the radius. Gravitation is closely related to circular motion as you will discover later.

Putting it all together m1m2 r2 G constant of proportionality Fg G Universal Gravitational Constant G 6.67 x10 Fg G 27 Nm 2 m1m2 r2 Fg mg Use this when you are on the earth Fg G m1m2 Use this when you are LEAVING th e earth r2 kg 2

Example: Let’s set the 2 equations equal to each other since they BOTH represent your weight or force due to gravity Fg mg Use this when you are on the earth Fg G m1m2 Use this when you are LEAVING th e earth 2 r Mm r2 M g G 2 r M Mass of the Earth 5.97 x1024 kg mg G r radius of the Earth 6.37 x106 m SOLVE FOR g! (6.67 x10 27 )(5.97 x10 24 ) g 9.81 m / s 2 6 2 (6.37 x10 )