Ant Colony Optimization Algorithms for the Traveling Salesman

Ant Colony Optimization Algorithms for the Traveling Salesman Problem ACO 3.1-3.5 Kristie Simpson EE536: Advanced Artificial Intelligence Montana State University

ACO Review Chapter 1: From Real to Artificial Ants (Dr. Paxton) – – – Looked at real ants and the double bridge experiment. Defined a stochastic model for real ants, and then modified the definition for artificial ants. Discussed the Simple-ACO algorithm.

ACO Review Chapter 2: The ACO Metaheuristic (Chris, Shen) – – – Introduced combinatorial optimization problems. Discussed exact and approximate solutions to NP-hard problems. Discussed the ACO Metaheuristic and example applications (TSP presented in section 2.3.1).

Chapter 3: ACO Algorithms for TSP “But you’re sixty years old. They can’t expect you to keep traveling every week.” –Linda in act I, scene I of Death of a Salesman, Authur Miller, 1949

Why use TSP? NP-Hard (permutation problem, N!). Easy application of ACO. Easy to understand. Ant System (the first ACO alogrithm) was tested on TSP. Solutions tend to be most efficient for other applications.

What is TSP? Starting from his hometown, a salesman wants to find a shortest tour that takes him through a given set of customer cities and then back home, visiting each customer city exactly once. Represented by a weighted graph G (N,A). The goal in TSP is to find a minimum length Hamiltonian circuit of the graph. An optimal solution is:

University of Heidelburg NAME : att532 TYPE : TSP COMMENT : 532-city problem (Padberg/Rinaldi) DIMENSION : 532 EDGE WEIGHT TYPE : ATT NODE COORD SECTION 1 7810 6053 2 7798 5709 3 7264 5575 4 7324 5560 5 7547 5503 6 7744 5476 7 7821 5457 8 7883 5408 att532 : 27686 http://www.iwr.uni-heidelberg.de/groups/comopt/software/TSPLIB95/

ACO Algorithms for the TSP G (C, L) is equal to G (N, A). All cities have to be visited and that each city is visited at most once. Pheromone trail: the desirability of visiting city j directly after i. Heuristic: inversely proportional to the distance between two cities i and j.

Tour Construction 1) 2) 3) Choose a start city. Use pheromone and heuristic values to add cites until all have been visited. Go back to the initial city. Note: Tour may be improved with a local search (section 3.7).

Skeleton for ACO algorithm Set parameters, initialize pheromone trails. While termination condition not met – – – ConstructAntSolutions ApplyLocalSearch UpdatePheromones Only solution construction and pheromone updates considered.

ACO Algorithms Ant System (AS) Elitist Ant System (EAS) Rank-Based Ant System (ASrank) Min-Max Ant System (MMAS) Ant Colony System (ACS) Approximate Nondeterministic Tree Search (ANTS) Hyper-Cube Framework for ACO

Ant System (AS) m ants concurrently build tour. Pheromone initialized to m/Cnn. Ants initially in randomly chosen sites. Random proportional rule used to decide which city to visit next. (see Box 3.1 for good parameter values)

Ant System (AS) Each ant k maintains a memory Mk for its neighborhood. After all ants have constructed their tours, the pheromone trails are updated. Pheromone evaporation:

Ant System (AS) Pheromone update:

Elitist Ant System (EAS) First improvement on AS. Provide strong additional reinforcement to the arcs belonging to the best tour found since the start of the algorithm.

Rank-Based Ant System (ASrank) Another improvement over AS. Each ant deposits an amount of pheromone that decreases with its rank. In each iteration, only the best (w-1) ranked ants and the best-so-far ant are allowed to deposit pheromone.

Min-Max Ant System (MMAS) Four – modifications with respect to AS. Strongly exploits the best tours found. This – – – may lead to stagnation. So Limits the possible range of pheromone values. Pheromone values initialized to upper limit. Pheromone values are reinitialized when system approaches stagnation.

Min-Max Ant System (MMAS) After all ants construct a solution, pheromone values are updated. (Evaporation is the same as in AS) Lower and upper limits on pheromones limit the probability of selecting a city. Initial pheromone values are set to the upper limit, resulting in initial exploration. Occasionally pheromones are reinitialized.

Ant Colony System (ACS) Uses ideas not included in the original AS. Differs from AS in three main points: – – – Exploits the accumulated search experience more strongly than AS. Pheromone evaporation and deposit take place only on the best-so-far tour. Each time an ant uses an arc, some pheromone is removed from the arc.

Ant Colony System (ACS) Pseudorandom proportional rule used to decide which city to visit next. Only best-so-far ant adds pheromone after each iteration. Evaporation and deposit only apply to best-so-far.

Ant Colony System (ACS) The previous pheromone update was global. Each ant in ACS also uses a local update that is applied after crossing an arc. Makes arc less desirable for following ants, increasing exploration.

Approximate Nondeterministic Tree Search (ANTS) Uses ideas not included in the original AS. Not applied to TSP. Computes lower bounds on the completion of a partial solution to define the heuristic information that is used by each ant during the solution construction. Creates a dynamic heuristic where the lower the estimate the more attractive the path.

Approximate Nondeterministic Tree Search (ANTS) Two modifications with respect to AS: – Use of a novel action choice rule. – Modified pheromone trail update rule. (No explicit pheromone evaporation)

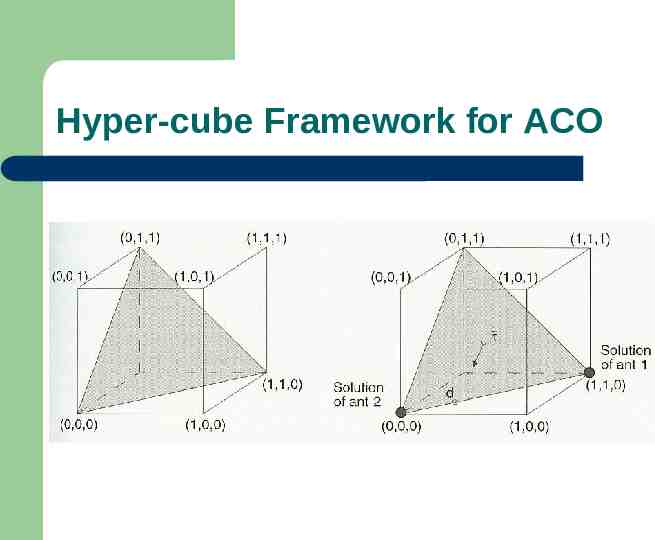
Hyper-cube Framework for ACO Uses ideas not included in the original AS. Not applied to TSP. Automatically rescales the pheromone values for them to lie always in the interval [0,1]. Decision variables {0, 1} typically correspond to the components used by the ants for construction. A solution problem then corresponds to one corner of the n-dimensional hyper-cube, where n is the number of decision variables.

Hyper-cube Framework for ACO

Parallel Implementation Fine-grained – few individuals per processor, frequent information exchange. – Can lead to major communication overhead. Coarse-grained – larger subpopulations per processor, information exchange is rare. – – Much more promising for ACO. p colonies on p processors.

Partially Asynchronous Parallel Implementation (PAPI) Information exchanged at fixed intervals. Studies show it is better to exchange the best solutions rather than all solutions.