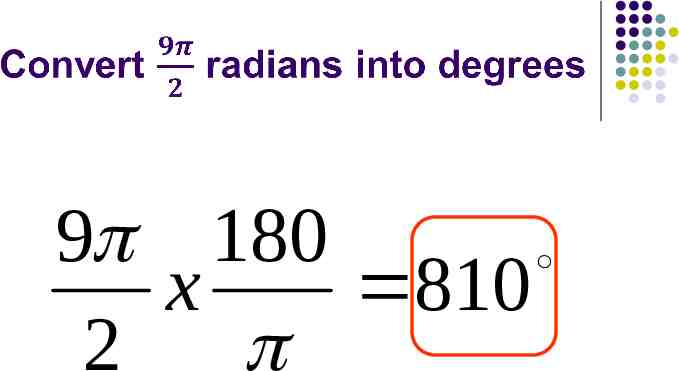Angles and their Measures Lesson 1

Angles and their Measures Lesson 1

As derived from the Greek Language, the word trigonometry means “measurement of triangles.” Initially, trigonometry dealt with relationships among the sides and angles of triangles and was used in the development of astronomy, navigation, and surveying.

With the development of Calculus and the physical sciences in the 17th Century, a different perspective arose – one that viewed the classic trigonometric relationships as functions with the set of real numbers as their domain. Consequently the applications expanded to include physical phenomena involving rotations and vibrations, including sound waves, light rays, planetary orbits, vibrating strings, pendulums, and orbits of atomic particles.

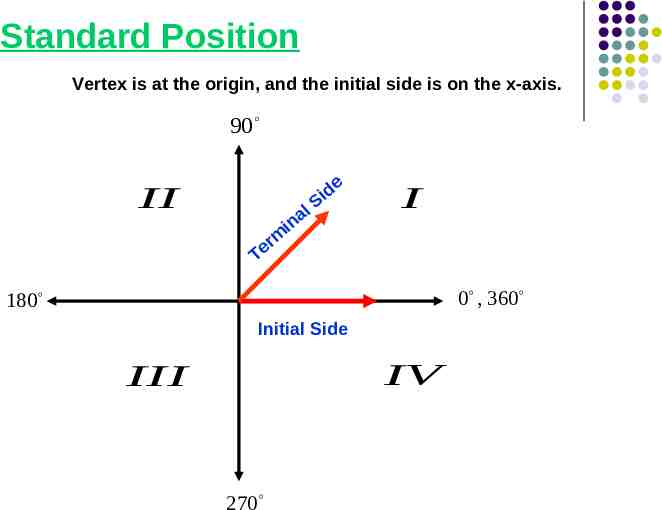
We will explore both perspectives beginning with angles and their measures . An angle is determined by rotating a ray about its endpoint. The starting position of called the initial side. The ending position is called the terminal side.

Standard Position Vertex is at the origin, and the initial side is on the x-axis. 90 II de i S l a in rm e T I 0 , 360 180 Initial Side IV III 270

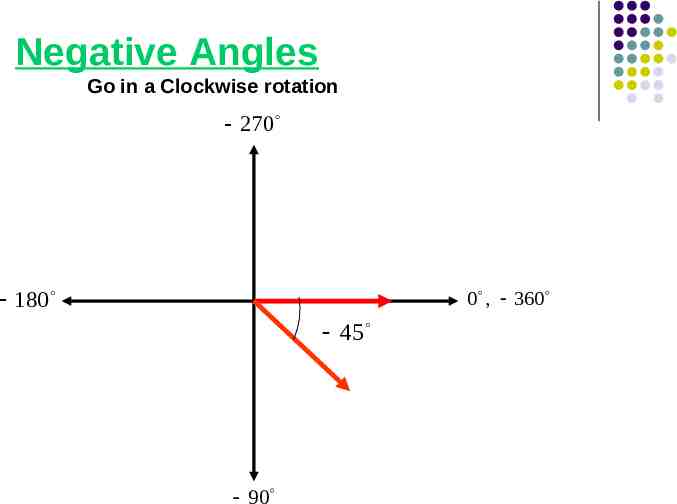
Positive Angles are generated by counterclockwise rotation. Negative Angles are generated by clockwise rotation. Let’s take a look at how negative angles are labeled on the coordinate graph.

Negative Angles Go in a Clockwise rotation 270 0 , 360 180 45 90

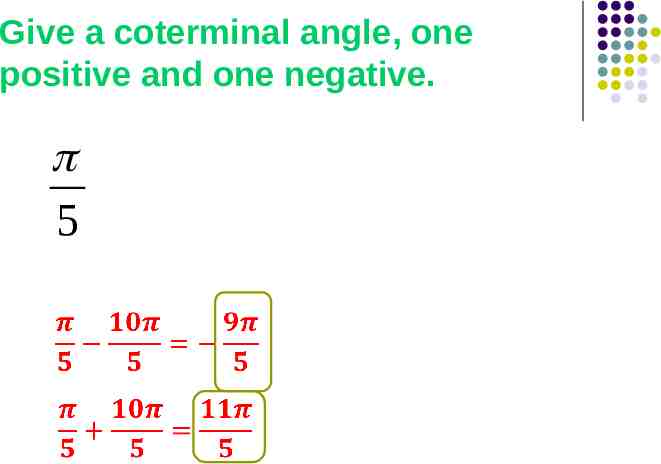
Coterminal Angles Angles that have the same initial and terminal side. See the examples below.

Coterminal Angles They have the same initial and terminal sides. Determine 2 coterminal angles, one positive and one negative for a 60 degree angle. 60 60 360 420 degrees 60 – 360 -300 degrees

Give 2 coterminal angles. 30 30 360 390 degrees 30 – 360 -330 degrees

Give a coterminal angle, one positive and one negative. 230 230 360 590 degrees 230 – 360 -130 degrees

Give a coterminal angle, one positive and one negative. 20 -20 360 340 degrees -20 – 360 -380 degrees

Give a coterminal angle, one positive and one negative. 460 460 360 820 degrees 460 – 360 100 degrees 100 – 360 -260 degrees Good but not best answer.

Complementary Angles Sum of the angles is 90 Find the complement of each angles: 40 40 x 90 x 50 degrees 120 No Complement!

Supplementary Angles Sum of the angles is 180 Find the supplement of each angles: 40 120 40 x 180 120 x 180 x 140 degrees x 60 degrees

Coterminal Angles: Angle 360 To find a Complementary Angle: To find a Supplementary Angle: 90 Angle 180 Angle

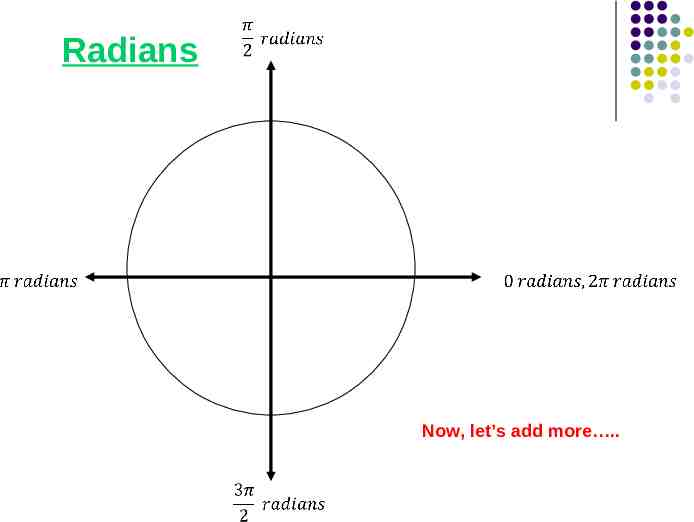
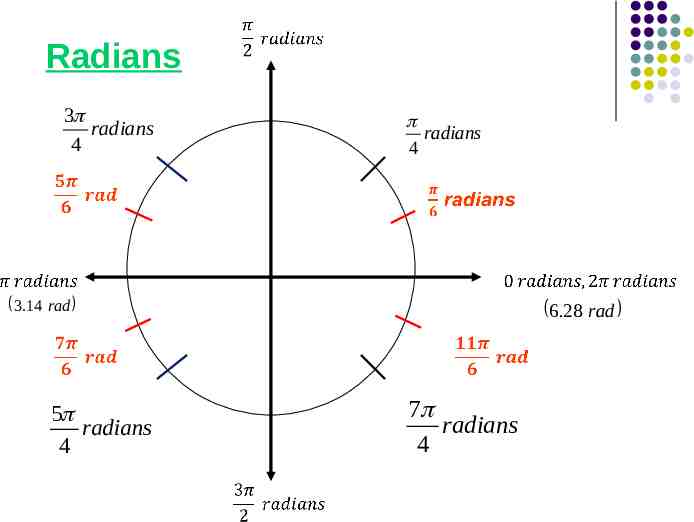
Radian Measure One radian is the measure of the central angle, , that intercepts an arc, s, that is equal in length to the radius r of the circle. C 2 r C 2 r 2 2 C r 2 So 1 revolution is equal to 2π radians

2 radians 360 radians 180 radians 90 2 Let’s take a look at them placed on the unit circle.

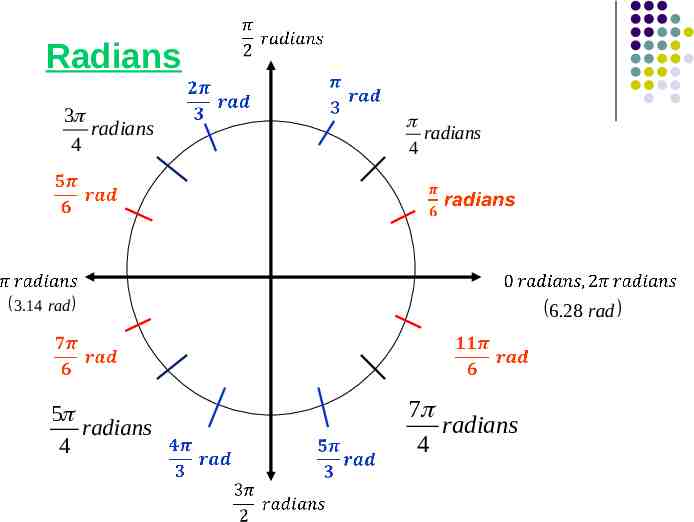
Radians Now, let’s add more .

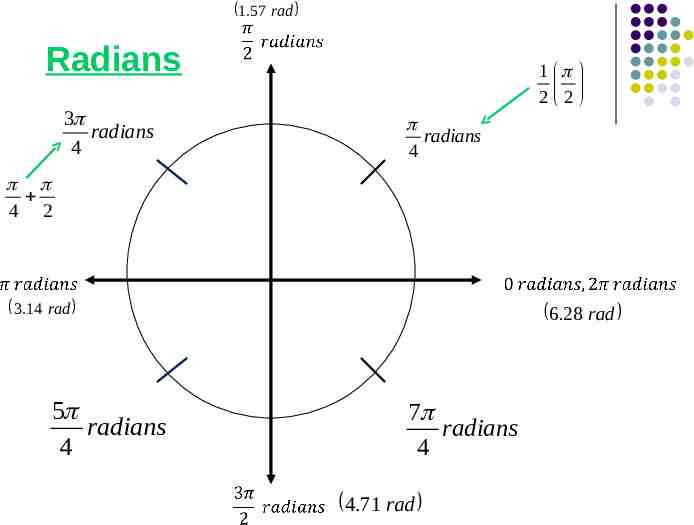
1.57 rad Radians 3 radians 4 1 2 2 radians 4 4 2 3.14 rad 5 radians 4 6.28 rad 7 radians 4 4.71 rad

More Common Angles Let’s take a look at more common angles that are found in the unit circle.

Radians 3 radians 4 radians 4 3.14 rad 5 radians 4 6.28 rad 7 radians 4

Radians 3 radians 4 radians 4 3.14 rad 5 radians 4 6.28 rad 7 radians 4

Look at the Quadrants

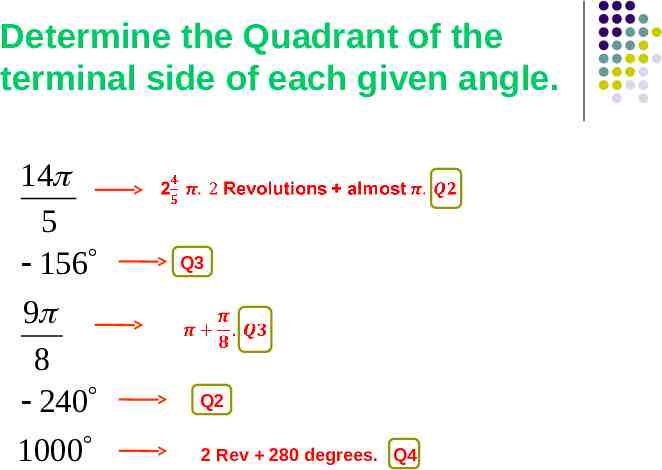
Determine the Quadrant of the terminal side of each given angle. 3 7 12 2 3 371 Q1 Go a little more than one quadrant – negative. Q3 A little more than one revolution. Q1

Determine the Quadrant of the terminal side of each given angle. 14 5 156 9 8 240 1000 Q3 Q2 2 Rev 280 degrees. Q4

Coterminal Angles using Radians

Find a coterminal angle. There are an infinite number of coterminal angles!

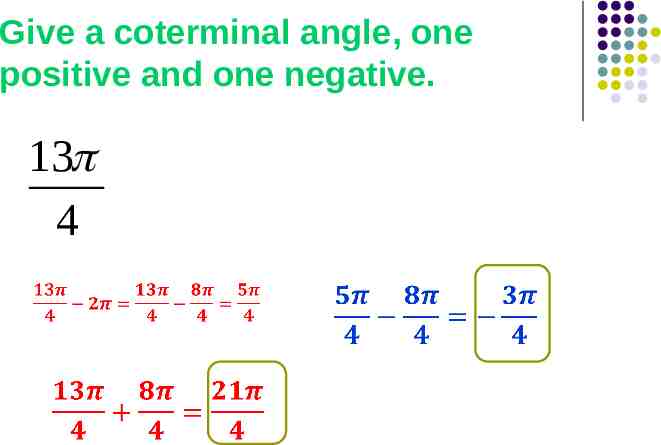
Give a coterminal angle, one positive and one negative. 13 4

Give a coterminal angle, one positive and one negative. 5

Find the complement of each angles: 2 5

Find the supplement of each angles: 2 5

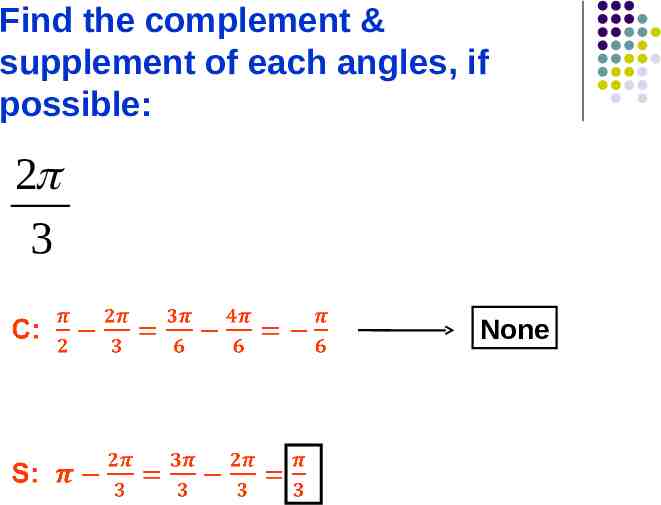
Find the complement & supplement of each angles, if possible: 2 3 None

Coterminal Angles: Angle 2 To find a Complementary Angle: Angle 2 To find a Supplementary Angle: Angle RECAP

Conversions 1 radians 180 180 1 radian

135 3 135 x 180 180 4 NOTE: The answer is in radians!

270 3 270 x 180 180 2

9 180 x 810 2

Convert 2 radians to degrees 180 360 2x 114.59

Arc Length The relationship between arc length, radius, and central angle is Arc Length (radius) (angle)

1st Change 240 degrees into radians. 240 4 240 x radians 180 180 3 4 s 4 3 16 s or 16.76 inches 3