Algorithms for Dynamic NFV Workload Seffi Naor .Computer Science Dept

Algorithms for Dynamic NFV Workload Seffi Naor .Computer Science Dept Technion Based on joint papers with Rami Cohen, Yaron Fairstain, Liane Lewin-Eytan, Danny Raz ]Infocom 2015, WAOA 2018[

Network Functions Virtualization (NFV) New way of designing, deploying, managing networking services. Decouples network functions from proprietary hardware appliances so they can run in software; e.g., network address translation (NAT), firewalling, intrusion detection, domain name service (DNS), parental control, caching, etc. Functions can be located in, e.g.,: servers at gateways, cloud (rental), private clouds (buying servers), edge compute (mobile edge computing)

Network Functions Virtualization (NFV) Challenging network design problems: how to support a fully virtualized infrastructure – including virtual servers, storage, other networks, etc. ? Leading to novel algorithmic location problems: – where? – how many locations? – which functions should be co-located? – taking into account: cost and capacity of infrastructure service chaining Ample work on facilty location – – yet focus has mostly been on a “single” function multi-commodity facility location [Ravi & Sinha, 2004]

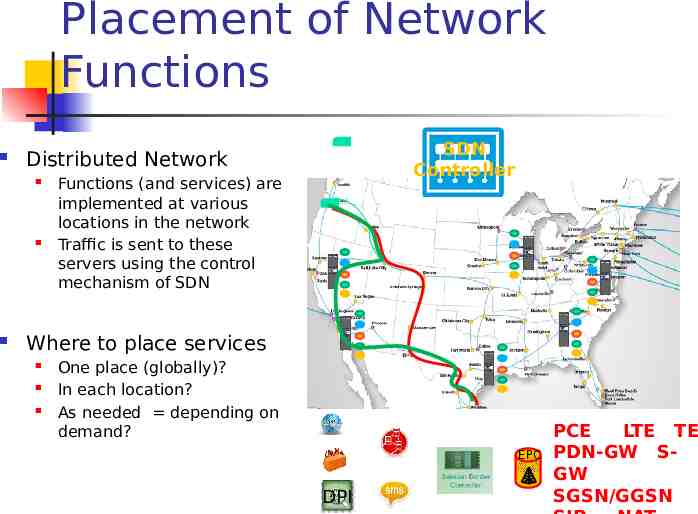
Placement of Network Functions SDN Controller Distributed Network Functions (and services) are implemented at various locations in the network Traffic is sent to these servers using the control mechanism of SDN Where to place services One place (globally)? In each location? As needed depending on demand? EPC DPI PCE LTE TE PDN-GW SGW SGSN/GGSN

Model: Problem Definition Input Network endowed with a distance metric d(·) Set of possible service locations Servers have bounded size For each network function: capacity - number of clients it can serve size on server setup cost Set of given flows (clients); for each flow: there is a predefined route in the network requests a set of network functions demand requirement for each function

Model: Problem Definition Output placement of network functions on servers rerouting of flow to network locations such that: demand of each flow is fully served by the functions it requested servers: size constraints are not exceeded by the functions placed at a server capacity constraints of each (copy of) function are met

Model: Problem Definition Objective function each flow is rerouted through servers containing the functions it requests functions are placed at the servers cost sum of distances from the flow path to the servers cost sum of setup costs of the functions setup cost is paid for each copy of a function total cost sum of distance costs sum of setup costs

Facility Location Problems Problem: network endowed with a distance metric set of clients facilities: each has a setup cost and capacity Goal: open a set of facilities in the network match clients to facilities while satisfying capacity constraints minimize sum of distance costs and setup costs History: classic problem, studied extensively since the 1960s NP-hard problem, constant-factor approximations In our terminology: single function!

Generalized Assignment Problem Jobs are assigned to machines: for each job: setup cost – machine dependent size – machine dependent for each machine: upper bound on total size of jobs assigned to it goal: minimize sum of setup costs, while satisfying size constraints In our terminology: multiple functions: job function infinite capacity - single copy of each function suffices network distances 0

NFV Location Problem Model captures important aspects of NFV placement A bi-criteria (O(1), O(1)) approximation algorithm for the general NFV location problem LP formulation of the problem rounding a fractional solution bi-criteria approximate solution: size constraints are violated by a constant Experimental results: significant improvement over greedy algorithm over many different scenarios Good performance in terms of obeying capacity constraints

Dynamic NFV Placement (1) from a “one shot” solution to an evolving solution setting: heterogeneous networks clients (flows) undergo changes, moving over time: e.g., satellites, mobile users highly dynamic in nature, therefore taking it into account is essential for efficient deployment

Dynamic NFV Placement (2) dynamic setting is captured by a metric evolving over time goal: allows us to model movement of flows over time computing a stable solution minimizing changes to the configuration, i.e., assignment changes demands and metric evolution are given ahead of time: prediction in HTS and vRAN systems is very useful

Dynamic Facility Location defined over a time horizon different metric at each time step change cost paid for assignment changes between consecutive time steps [Eisenstat, Mathieu, Schabanel, ICALP 2014]

Model: Problem Definition Input Time horizon T Metric changes at each time step: Servers remain at fixed locations Clients are dynamically changing location Cost g for client assignment changes between time steps Set of possible service locations Servers have bounded size Set of given flows (clients); for each flow: there is a predefined route in the network for each time step requests a set of network functions demand requirement for each function

Model: Problem Definition Output placement of network functions on servers rerouting of flow to network locations such that: demand of each flow is fully served by the functions it requested at each time step servers: size constraints are not exceeded by the functions placed at a server capacity constraints of each (copy of) function are met

Model: Problem Definition Objective function each flow is rerouted through servers containing the functions it requests functions are placed at the servers connection cost sum of distances from the flow path to the servers change cost number of assignment changes times the change cost cost sum of setup costs of the functions setup cost is paid for each copy of a function total cost sum of distance costs sum of setup costs sum of change costs

Dynamic NFV Interval selection: Independently, for each client and function breaks time horizon into intervals with fixed fractional assignment at most doubles fractional solution guarantees fractional change of at least over each interval

Interval Graph List Coloring Input interval graph a set of colors for each interval – a subset of colors it can be legally colored with Output a legal coloring of the intervals such that intersecting intervals are colored differently

Interval Graph List Coloring List coloring is NP-hard even on interval graphs (unlike coloring) Goal: minimizing the number of “extra” copies of any color we show an integrality gap of where is the size of the largest clique in the interval graph we show how to color the intervals with at most copies of each color, given that a feasible fractional coloring exists

IGLC - Approximation Consider a bipartite graph – intervals at a specific point – colors - edges between intervals to colors they can be colored with In any feasible fractional coloring each subset of intervals is colored with at least colors Each subset can be colored with at least colors can be fully matched to colors (Hall’s theorem)

Dynamic NFV Define an instance of IGLC: each ball with capacity colors each interval can be colored with colors belonging to its representative balls

Dynamic NFV - Analysis Setup part placing a function for each ball using GAP rounding factor of 2 to the size violation Overall demand of each client is fully satisfied constant factor approximation of the cost constant factor violation of size constraints logarithmic factor violation of capacity constraints

23