A Global Linear Method for Camera Pose Registration Nianjuan Jiang*1,

A Global Linear Method for Camera Pose Registration Nianjuan Jiang*1, Zhaopeng Cui*2, Ping Tan2 1 Advanced Digital Sciences Center, Singapore 2 National University of Singapore *Joint first authors 1

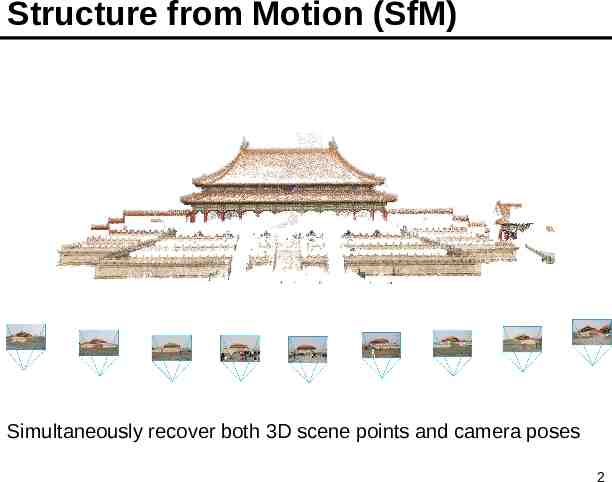
Structure from Motion (SfM) Simultaneously recover both 3D scene points and camera poses 2

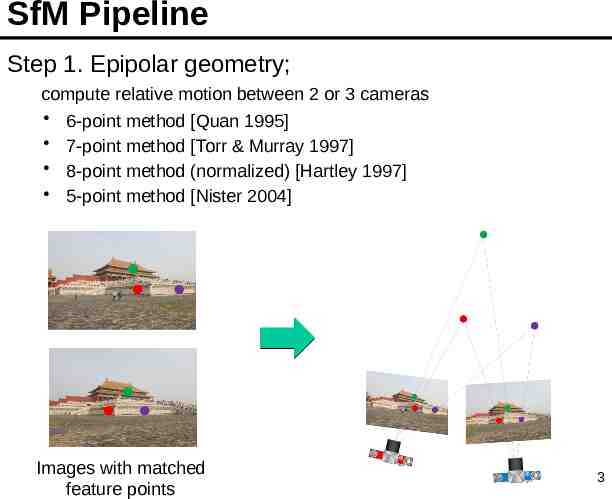
SfM Pipeline Step 1. Epipolar geometry; compute relative motion between 2 or 3 cameras 6-point method [Quan 1995] 7-point method [Torr & Murray 1997] 8-point method (normalized) [Hartley 1997] 5-point method [Nister 2004] Images with matched feature points 3

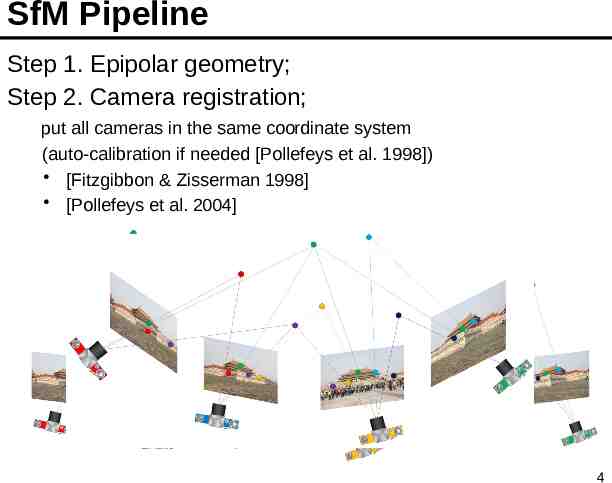
SfM Pipeline Step 1. Epipolar geometry; Step 2. Camera registration; put all cameras in the same coordinate system (auto-calibration if needed [Pollefeys et al. 1998]) [Fitzgibbon & Zisserman 1998] [Pollefeys et al. 2004] 4

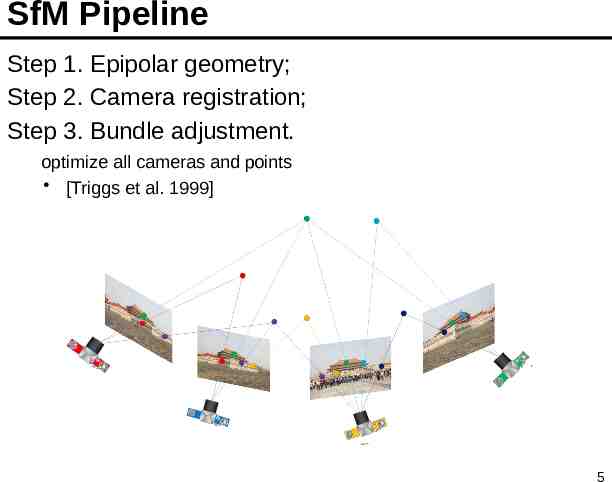
SfM Pipeline Step 1. Epipolar geometry; Step 2. Camera registration; Step 3. Bundle adjustment. optimize all cameras and points [Triggs et al. 1999] 5

“The Black Art ” Step 1. Epipolar geometry; Step 2. Camera registration; Step 3. Bundle adjustment. The state-of-the-art: 1. Step 1 and 3 are very well studied with elegant theories and algorithms. 2. The step 2 is often ad-hoc and heuristic. The camera registration to initialize bundle adjustment “ is still to some extent a black art ”. Page 452, Chapter 18.6 6

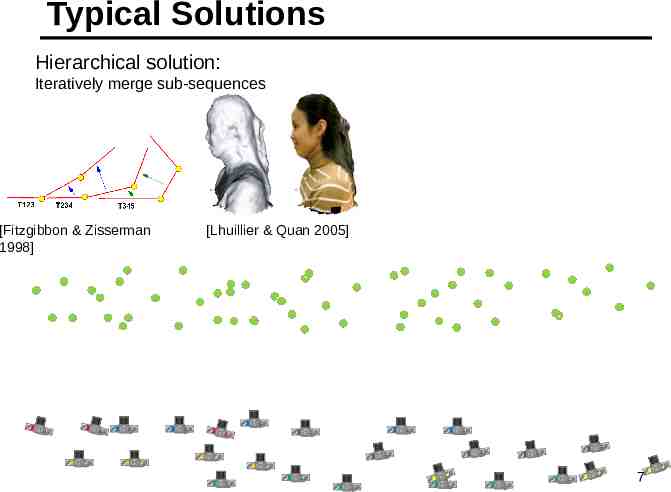
Typical Solutions Hierarchical solution: Iteratively merge sub-sequences [Fitzgibbon & Zisserman 1998] [Lhuillier & Quan 2005] 7

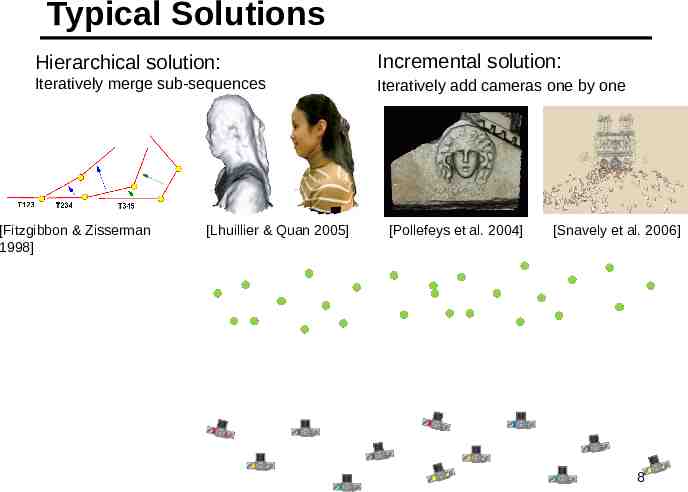
Typical Solutions Hierarchical solution: Incremental solution: Iteratively merge sub-sequences Iteratively add cameras one by one [Fitzgibbon & Zisserman 1998] [Lhuillier & Quan 2005] [Pollefeys et al. 2004] [Snavely et al. 2006] 8

Pain of Existing Solutions The block diagram (for the incremental solution): Step 1: Epipolar Geometry Initial Reconstruction (2 cameras) Register All Cameras in a Single Step Add Cameras Bundle Adjustment More Cameras? Step 3: Bundle Adjustment Drawbacks: 1. Repetitively calling bundle adjustment Inefficiency Ourtime objective: 90% of the total computation is spent on bundle adjustment. Simultaneously register cameras to initialize 2. Some cameras are fixed before theallothers bundle adjustment asymmetric formulationthe leads to inferior results. 9

Previous Works linear global solution to rotations cannot solve translations discrete-continuous optimization require coplanar cameras [Govindu 2001] [Hartley etfeatures: al. 2013] Desirable [Crandall et al. 2011] 1. Solve both rotations & translations; 2. Linear & robust solution; elegant quasi-convex optimization linear global solution to translations 3. No degeneracy. sensitive to outliers L [Kahl 2005] [Martinec et al. 2007] degenerate at collinear motion [Arie-Nachimson et al. 2012] 10

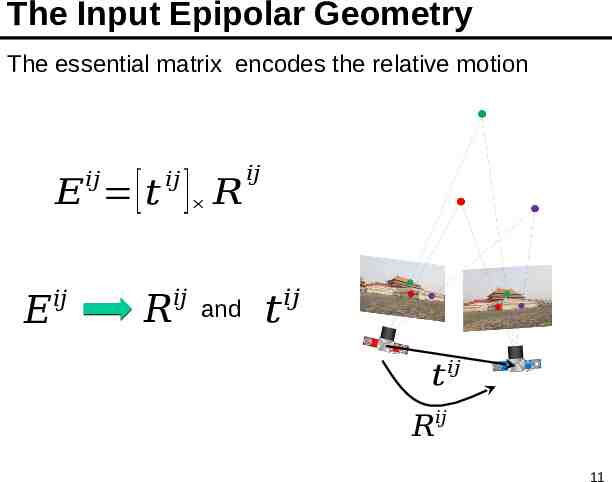
The Input Epipolar Geometry The essential matrix encodes the relative motion 𝑖𝑗 𝐸 [ 𝑡 𝐸 𝑖𝑗 𝑖𝑗 𝑅 ] 𝑅 𝑖𝑗 and 𝑖𝑗 𝑡 𝑖𝑗 𝑡 𝑖𝑗 𝑅𝑖𝑗 11

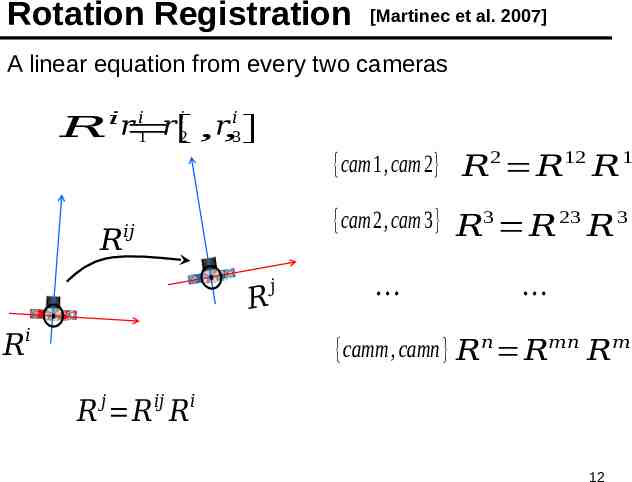
Rotation Registration [Martinec et al. 2007] A linear equation from every two cameras 𝑖 𝑖 𝑖 𝑖 𝑟 𝑟 𝑟 𝑅 [ 1 2 , ,3] {cam1,cam 2} 𝑅2 𝑅12 𝑅 1 𝑅𝑖𝑗 𝑅𝑖 𝑅 𝑗 {cam2,cam 3} 𝑅 𝑅 𝑅 3 23 3 {camm, camn} 𝑅𝑛 𝑅𝑚𝑛 𝑅𝑚 𝑗 𝑖𝑗 𝑅 𝑅 𝑅 𝑖 12

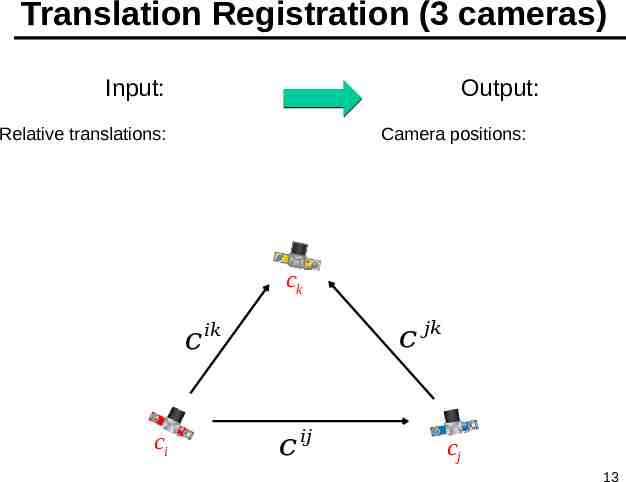
Translation Registration (3 cameras) Input: Output: Relative translations: Camera positions: ck 𝑐 ci 𝑐 𝑗𝑘 𝑖𝑘 𝑐 𝑖𝑗 cj 13

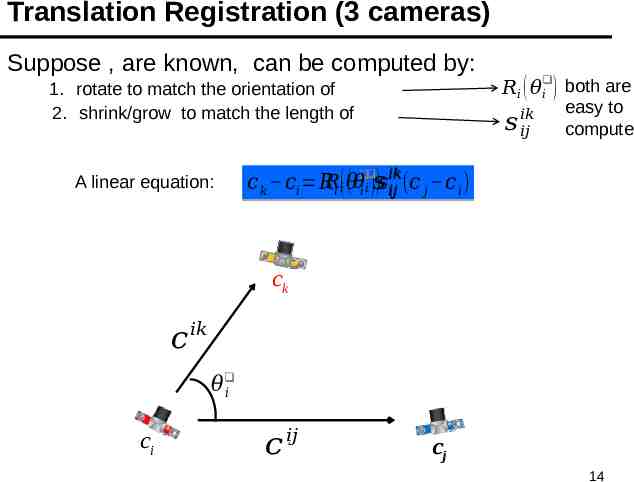
Translation Registration (3 cameras) Suppose , are known, can be computed by: 1. rotate to match the orientation of 2. shrink/grow to match the length of A linear equation: 𝑅𝑖 ( 𝜃𝑖 ) both are 𝑠 𝑖𝑘 𝑖𝑗 easy to compute 𝑖𝑘 𝑖𝑘 𝑐 𝑘 𝑐𝑖 𝑅𝑅𝑖 (𝑖 𝜃 ( 𝜃 𝑖 𝑖 )𝑠)𝑠𝑖𝑗𝑖𝑘𝑖𝑗 (𝑐 𝑗 𝑐 𝑖 ) ck 𝑐 𝑖𝑘 𝜃 𝑖 ci 𝑐 𝑖𝑗 cj 14

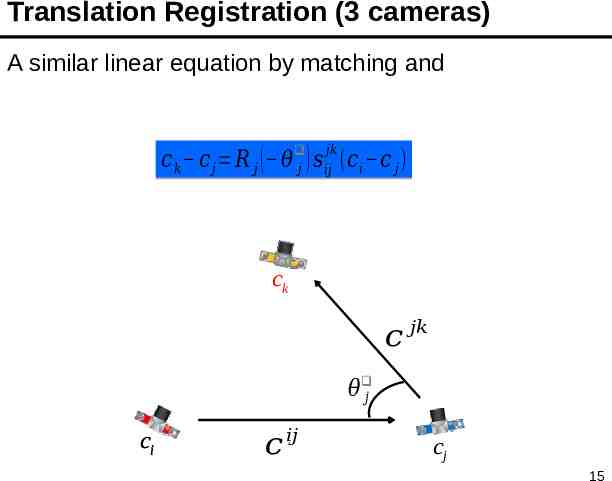
Translation Registration (3 cameras) A similar linear equation by matching and 𝑗𝑘 𝑐 𝑘 𝑐 𝑗 𝑅 𝑗 ( 𝜃 𝑗 ) 𝑠 𝑖𝑗𝑗𝑘 (𝑐 𝑖 𝑐 𝑗 ) ck 𝑐 𝑗𝑘 𝜃 𝑗 ci 𝑐 𝑖𝑗 cj 15

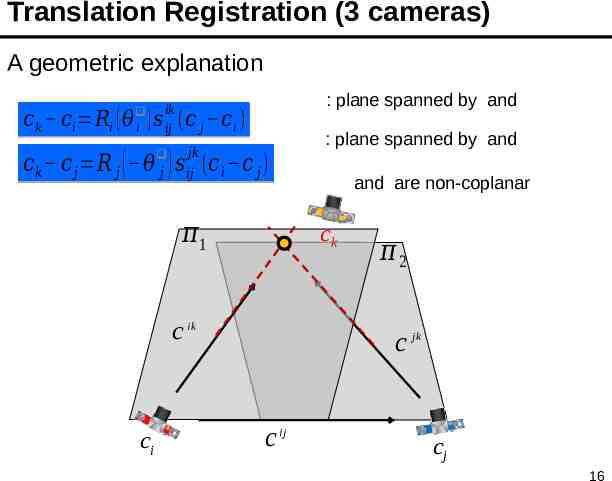
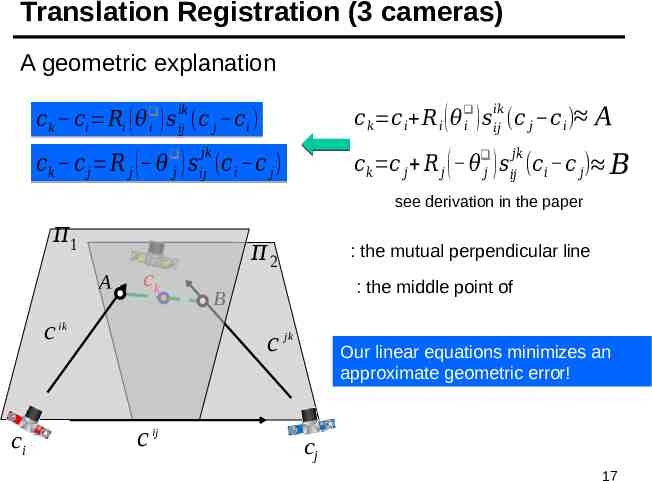
Translation Registration (3 cameras) A geometric explanation : plane spanned by and 𝑖𝑘 𝑖𝑗 𝑐 𝑘 𝑐𝑖 𝑅𝑖 ( 𝜃 ) 𝑠 (𝑐 𝑗 𝑐 𝑖 ) 𝑖 : plane spanned by and 𝑗𝑘 𝑖𝑗 𝑐 𝑘 𝑐 𝑗 𝑅 𝑗 ( 𝜃 ) 𝑠 (𝑐 𝑖 𝑐 𝑗 ) 𝑗 𝜋1 ck c ik ci and are non-coplanar 𝜋2 c jk c ij cj 16

Translation Registration (3 cameras) A geometric explanation 𝑐 𝑘 𝑐 𝑖 𝑅 𝑖 ( 𝜃 𝑖 ) 𝑠 𝑖𝑗 (𝑐 𝑗 𝑐 𝑖 ) 𝑖𝑘 𝑖𝑘 𝑐 𝑘 𝑐𝑖 𝑅𝑖 ( 𝜃 𝑖 ) 𝑠 𝑖𝑘 (𝑐 𝑗 𝑐 𝑖 ) 𝑖𝑗 𝑗𝑘 𝑐 𝑘 𝑐 𝑗 𝑅 𝑗 ( 𝜃 𝑗 ) 𝑠 𝑖𝑗𝑗𝑘 (𝑐 𝑖 𝑐 𝑗 ) A 𝑗𝑘 𝑖𝑗 𝑐 𝑘 𝑐 𝑗 𝑅 𝑗 ( 𝜃 ) 𝑠 (𝑐 𝑖 𝑐 𝑗 ) 𝐵 𝑗 see derivation in the paper 𝜋1 A ck c ik ci 𝜋2 : the mutual perpendicular line : the middle point of B c jk c ij Our linear equations minimizes an approximate geometric error! cj 17

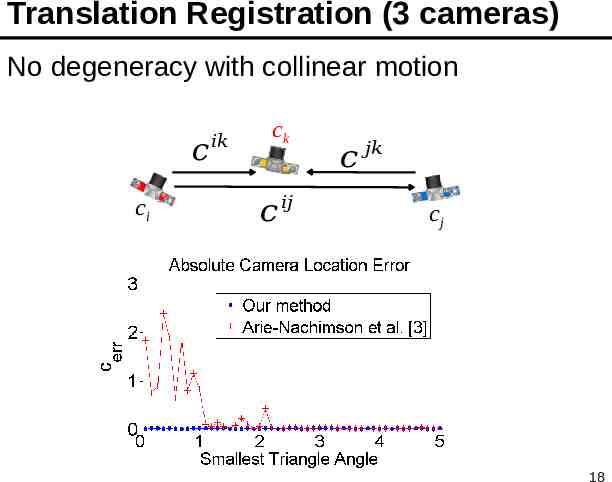
Translation Registration (3 cameras) No degeneracy with collinear motion 𝑐 ci 𝑖𝑘 ck 𝑐 𝑐 𝑗𝑘 𝑖𝑗 cj 𝑖𝑘 𝑐 𝑘 𝑐𝑖 𝑅𝑖 ( 0 ) 𝑠 𝑖𝑘 𝑖𝑗 (𝑐 𝑗 𝑐 𝑖 ) 𝑗𝑘 𝑖𝑗 𝑐 𝑘 𝑐 𝑗 𝑅 𝑗 ( 0 ) 𝑠 (𝑐𝑖 𝑐 𝑗 ) 18

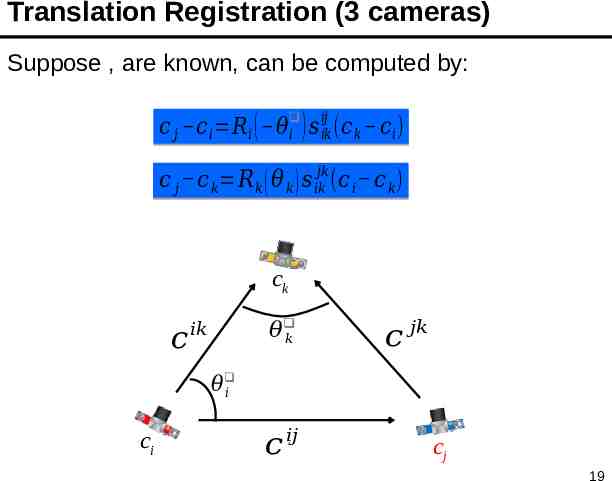
Translation Registration (3 cameras) Suppose , are known, can be computed by: 𝑖𝑗 𝑐 𝑗 𝑐 𝑖 𝑅𝑖 ( 𝜃 𝑖 ) 𝑠 𝑖𝑗𝑖𝑘 (𝑐 𝑘 𝑐𝑖 ) 𝑐 𝑗 𝑐 𝑘 𝑅 𝑘 ( 𝜃 𝑘 ) 𝑠 𝑖𝑘𝑗𝑘 (𝑐 𝑖 𝑐 𝑘) ck 𝑐 𝜃 𝑘 𝑖𝑘 𝑐 𝑗𝑘 𝜃 𝑖 ci 𝑐 𝑖𝑗 cj 19

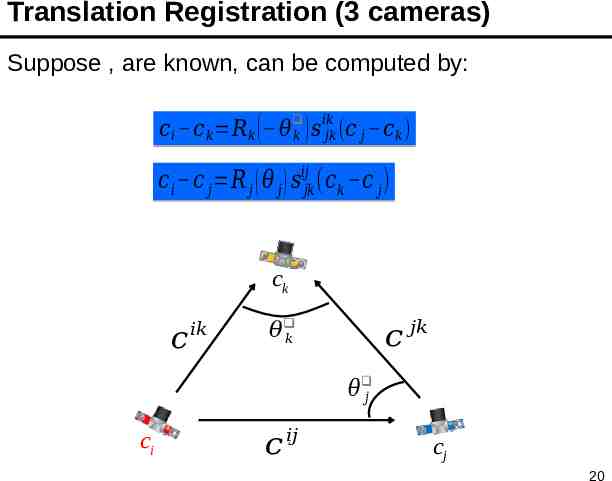
Translation Registration (3 cameras) Suppose , are known, can be computed by: 𝑐 𝑖 𝑐 𝑘 𝑅 𝑘 ( 𝜃 𝑘 ) 𝑠 𝑖𝑘𝑗𝑘 (𝑐 𝑗 𝑐 𝑘 ) 𝑐 𝑖 𝑐 𝑗 𝑅 𝑗 ( 𝜃 𝑗 ) 𝑠𝑖𝑗𝑗𝑘 (𝑐𝑘 𝑐 𝑗 ) ck 𝑐 𝑖𝑘 𝑐 𝑗𝑘 𝜃 𝑘 𝜃 𝑗 ci 𝑐 𝑖𝑗 cj 20

Translation Registration (3 cameras) Collecting all six equations 𝐵𝑖𝑗𝑘 𝑐𝑖 𝑐 𝑗 0 𝑐𝑘 ( ) 21

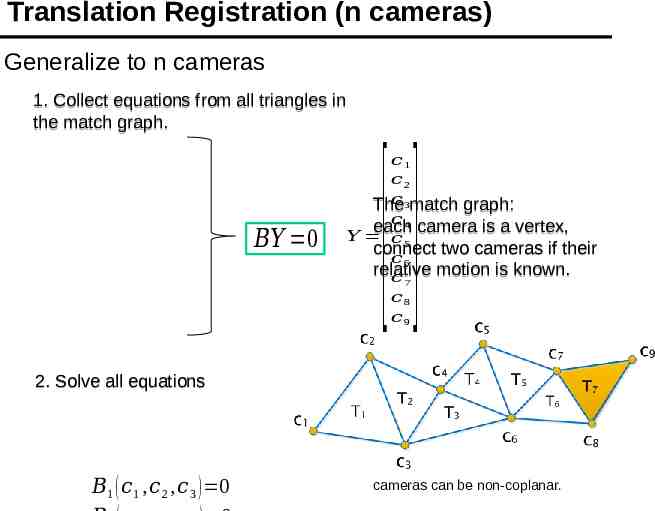
Translation Registration (n cameras) Generalize to n cameras 1. Collect equations from all triangles in the match graph. 𝐵𝑌 0 𝑐1 𝑐2 𝑐 3match graph: The 𝑐4 each camera is a vertex, 𝑌 𝑐5 connect two cameras if their 𝑐6 relative motion is known. 𝑐7 𝑐8 𝑐9 [] 2. Solve all equations 𝐵1 ( 𝑐1 , 𝑐 2 , 𝑐 3 ) 0 cameras can be non-coplanar.

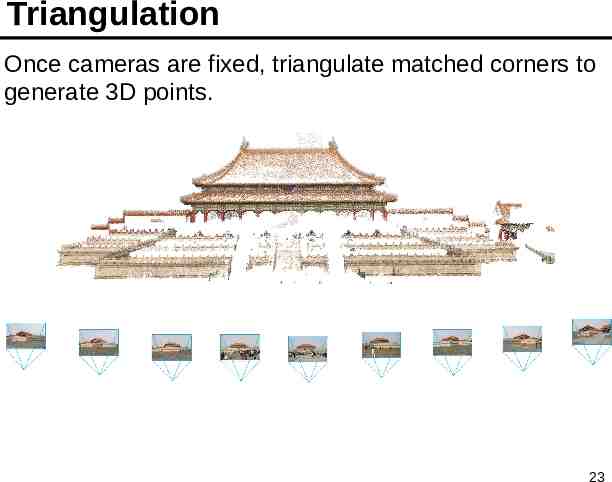
Triangulation Once cameras are fixed, triangulate matched corners to generate 3D points. 23

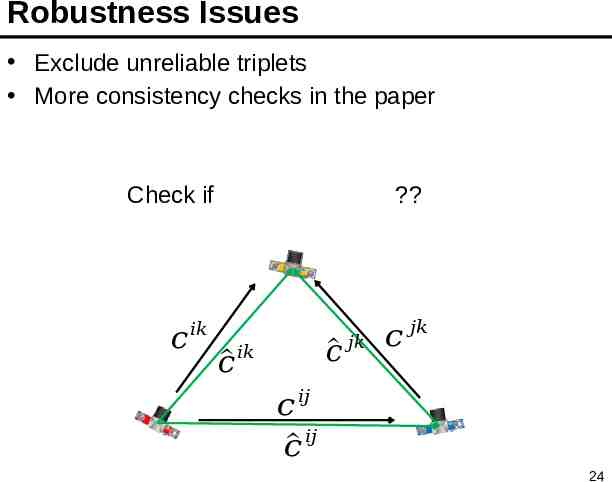
Robustness Issues Exclude unreliable triplets More consistency checks in the paper Check if 𝑐 ? 𝑖𝑘 𝑐 𝑗𝑘 𝑐 𝑖𝑘 𝑐 𝑗𝑘 𝑐 𝑖𝑗 𝑖𝑗 𝑐 24

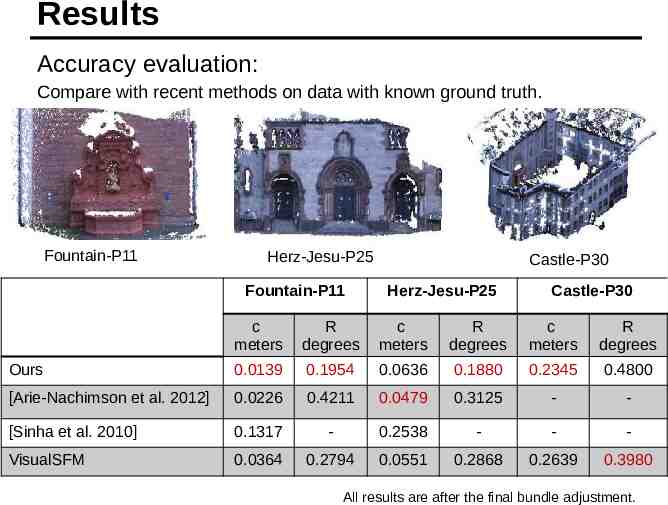
Results Accuracy evaluation: Compare with recent methods on data with known ground truth. Fountain-P11 Herz-Jesu-P25 Fountain-P11 Castle-P30 Herz-Jesu-P25 Castle-P30 c meters R degrees c meters R degrees c meters R degrees Ours 0.0139 0.1954 0.0636 0.1880 0.2345 0.4800 [Arie-Nachimson et al. 2012] 0.0226 0.4211 0.0479 0.3125 - - [Sinha et al. 2010] 0.1317 - 0.2538 - - - VisualSFM 0.0364 0.2794 0.0551 0.2868 0.2639 0.3980 All results are after the final bundle adjustment.

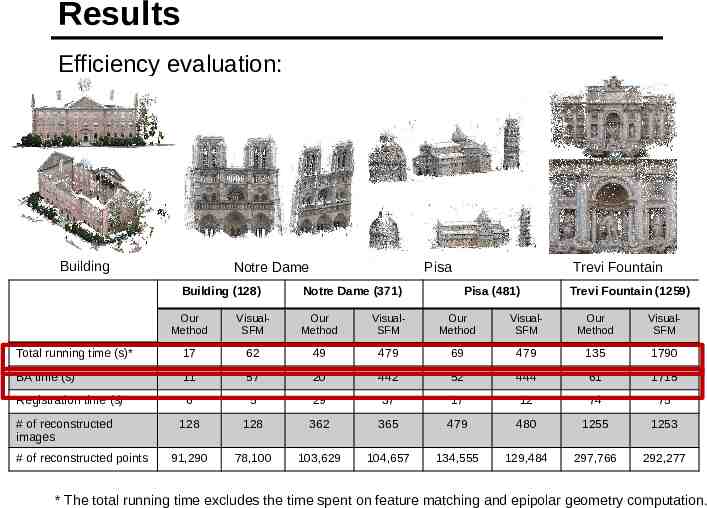
Results Efficiency evaluation: Building Notre Dame Building (128) Pisa Notre Dame (371) Trevi Fountain Pisa (481) Trevi Fountain (1259) Our Method VisualSFM Our Method VisualSFM Our Method VisualSFM Our Method VisualSFM Total running time (s)* 17 62 49 479 69 479 135 1790 BA time (s) 11 57 20 442 52 444 61 1715 Registration time (s) 6 5 29 37 17 12 74 75 128 128 362 365 479 480 1255 1253 91,290 78,100 103,629 104,657 134,555 129,484 297,766 292,277 # of reconstructed images # of reconstructed points * The total running time excludes the time spent on feature matching and epipolar geometry computation.

Conclusions A global solution for orientations & positions; Linear, robust & geometrically meaningful; No degeneracy. 27

Thanks! code & data available at: http://www.ece.nus.edu.sg/stfpage/eletp/

Results A large scale scene Quasi-dense points generated by CMVS [Furukawa et al. 2010] for better visualization. 29