9-1 9-1Geometric GeometricSequences Sequences Warm Up

9-1 9-1Geometric GeometricSequences Sequences Warm Up Lesson Presentation Lesson Quiz Holt Holt McDougal Algebra 1Algebra Algebra11 Holt McDougal

9-1 Geometric Sequences Warm Up Find the value of each expression. 1. 25 3. –34 32 2. 2–5 –81 5. (0.2)3 0.008 7. Holt McDougal Algebra 1 4. (–3)4 6. 7(–4)2 81 112 8. 12(–0.4)3 –0.768

9-1 Geometric Sequences Objectives Recognize and extend geometric sequences. Find the nth term of a geometric sequence. Holt McDougal Algebra 1

9-1 Geometric Sequences Vocabulary geometric sequence common ratio Holt McDougal Algebra 1

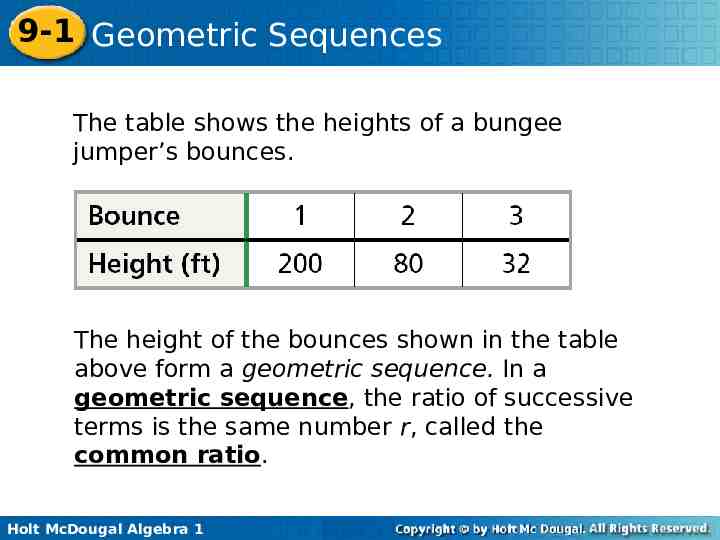
9-1 Geometric Sequences The table shows the heights of a bungee jumper’s bounces. The height of the bounces shown in the table above form a geometric sequence. In a geometric sequence, the ratio of successive terms is the same number r, called the common ratio. Holt McDougal Algebra 1

9-1 Geometric Sequences Geometric sequences can be thought of as functions. The term number, or position in the sequence, is the input, and the term itself is the output. 1 2 3 4 3 6 12 24 a1 a2 a3 a4 Position Term To find a term in a geometric sequence, multiply the previous term by r. Holt McDougal Algebra 1

9-1 Geometric Sequences Holt McDougal Algebra 1

9-1 Geometric Sequences Writing Math The variable a is often used to represent terms in a sequence. The variable a4 (read “a sub 4”)is the fourth term in a sequence. Holt McDougal Algebra 1

9-1 Geometric Sequences Example 1A: Extending Geometric Sequences Find the next three terms in the geometric sequence. 1, 4, 16, 64, Step 1 Find the value of r by dividing each term by the one before it. 1 4 16 64 The value of r is 4. Holt McDougal Algebra 1

9-1 Geometric Sequences Example 1A Continued Find the next three terms in the geometric sequence. 1, 4, 16, 64, Step 2 Multiply each term by 4 to find the next three terms. 64 256 4 1024 4 4096 4 The next three terms are 256, 1024, and 4096. Holt McDougal Algebra 1

9-1 Geometric Sequences Example 1B: Extending Geometric Sequences Find the next three terms in the geometric sequence. Step 1 Find the value of r by dividing each term by the one before it. – Holt McDougal Algebra 1 The value of r is .

9-1 Geometric Sequences Helpful Hint When the terms in a geometric sequence alternate between positive and negative, the value of r is negative. Holt McDougal Algebra 1

9-1 Geometric Sequences Example 1B Continued Find the next three terms in the geometric sequence. Step 2 Multiply each term by three terms. The next three terms are Holt McDougal Algebra 1 to find the next

9-1 Geometric Sequences Check It Out! Example 1a Find the next three terms in the geometric sequence. 5, –10, 20,–40, Step 1 Find the value of r by dividing each term by the one before it. 5 –10 20 –40 The value of r is –2. Holt McDougal Algebra 1

9-1 Geometric Sequences Check It Out! Example 1a Continued Find the next three terms in the geometric sequence. 5, –10, 20,–40, Step 2 Multiply each term by –2 to find the next three terms. –40 80 –160 320 (–2) (–2) (–2) The next three terms are 80, –160, and 320. Holt McDougal Algebra 1

9-1 Geometric Sequences Check It Out! Example 1b Find the next three terms in the geometric sequence. 512, 384, 288, Step 1 Find the value of r by dividing each term by the one before it. 512 384 288 The value of r is 0.75. Holt McDougal Algebra 1

9-1 Geometric Sequences Check It Out! Example 1b Continued Find the next three terms in the geometric sequence. 512, 384, 288, Step 2 Multiply each term by 0.75 to find the next three terms. 288 216 162 121.5 0.75 0.75 0.75 The next three terms are 216, 162, and 121.5. Holt McDougal Algebra 1

9-1 Geometric Sequences To find the output an of a geometric sequence when n is a large number, you need an equation, or function rule. The pattern in the table shows that to get the nth term, multiply the first term by the common ratio raised to the power n – 1. Holt McDougal Algebra 1

9-1 Geometric Sequences If the first term of a geometric sequence is a1, the nth term is an , and the common ratio is r, then an a1rn–1 nth term Holt McDougal Algebra 1 1st term Common ratio

9-1 Geometric Sequences Example 2A: Finding the nth Term of a Geometric Sequence The first term of a geometric sequence is 500, and the common ratio is 0.2. What is the 7th term of the sequence? an a1rn–1 Write the formula. a7 500(0.2)7–1 Substitute 500 for a1,7 for n, and 0.2 for r. Simplify the exponent. 500(0.2)6 Use a calculator. 0.032 The 7th term of the sequence is 0.032. Holt McDougal Algebra 1

9-1 Geometric Sequences Example 2B: Finding the nth Term of a Geometric Sequence For a geometric sequence, a1 5, and r 2. Find the 6th term of the sequence. an a1rn–1 Write the formula. a6 5(2)6–1 Substitute 5 for a1,6 for n, and 2 for r. Simplify the exponent. 5(2)5 160 The 6th term of the sequence is 160. Holt McDougal Algebra 1

9-1 Geometric Sequences Example 2C: Finding the nth Term of a Geometric Sequence What is the 9th term of the geometric sequence 2, –6, 18, –54, ? 2 –6 18 –54 The value of r is –3. an a1rn–1 a9 2(–3)9–1 Write the formula. Substitute 2 for a1,9 for n, and –3 for r. Simplify the exponent. Use a calculator. 2(–3)8 13,122 The 9th term of the sequence is 13,122. Holt McDougal Algebra 1

9-1 Geometric Sequences Caution When writing a function rule for a sequence with a negative common ratio, remember to enclose r in parentheses. –212 (–2)12 Holt McDougal Algebra 1

9-1 Geometric Sequences Check It Out! Example 2 What is the 8th term of the sequence 1000, 500, 250, 125, ? 1000 500 250 125 The value of r is an a1rn–1 Write the formula. a8 1000( )8–1 Substitute 1000 for a1,8 for n, and for r. Simplify the exponent. 7.8125 Use a calculator. The 8th term of the sequence is 7.8125. Holt McDougal Algebra 1 .

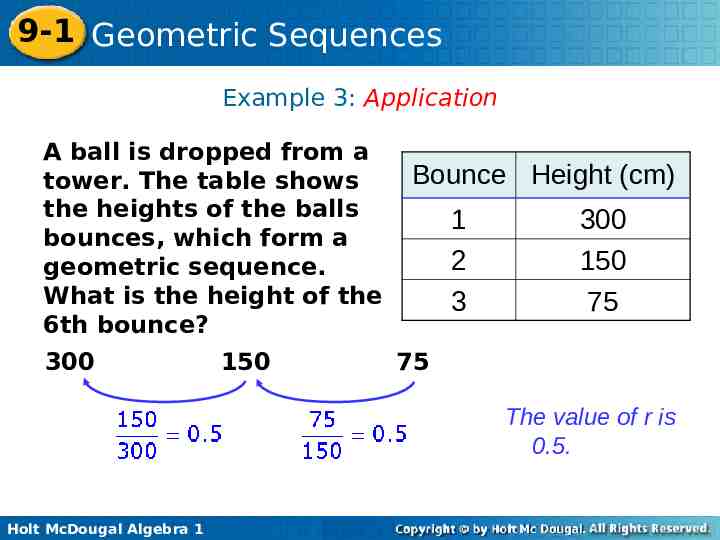
9-1 Geometric Sequences Example 3: Application A ball is dropped from a tower. The table shows the heights of the balls bounces, which form a geometric sequence. What is the height of the 6th bounce? 300 150 Bounce Height (cm) 1 2 3 300 150 75 75 The value of r is 0.5. Holt McDougal Algebra 1

9-1 Geometric Sequences Example 3 Continued an a1rn–1 Write the formula. a6 300(0.5)6–1 Substitute 300 for a1, 6 for n, and 0.5 for r. 300(0.5)5 Simplify the exponent. 9.375 Use a calculator. The height of the 6th bounce is 9.375 cm. Holt McDougal Algebra 1

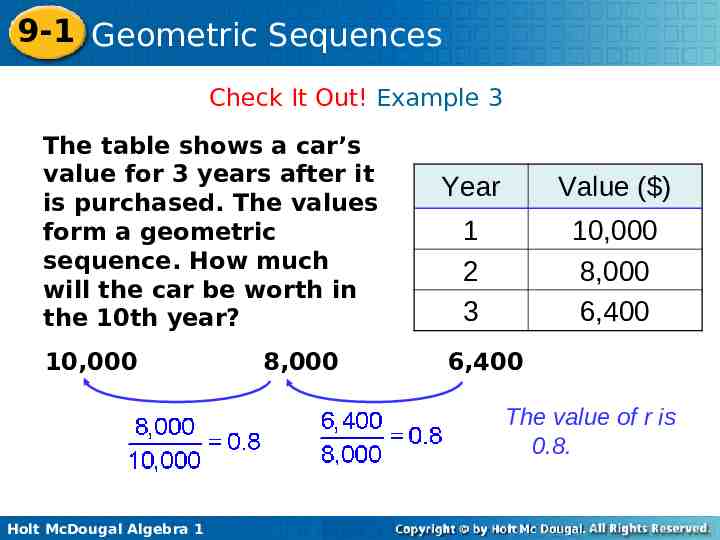
9-1 Geometric Sequences Check It Out! Example 3 The table shows a car’s value for 3 years after it is purchased. The values form a geometric sequence. How much will the car be worth in the 10th year? 10,000 8,000 Year Value ( ) 1 2 3 10,000 8,000 6,400 6,400 The value of r is 0.8. Holt McDougal Algebra 1

9-1 Geometric Sequences Check It Out! Example 3 an a1rn–1 Write the formula. a6 10,000(0.8)10–1 Substitute 10,000 for a1,10 for n, and 0.8 for r. 10,000(0.8)9 Simplify the exponent. 1,342.18 Use a calculator. In the 10th year, the car will be worth 1342.18. Holt McDougal Algebra 1

9-1 Geometric Sequences Lesson Quiz: Part I Find the next three terms in each geometric sequence. 1. 3, 15, 75, 375, 1875; 9375; 46,875 2. 3. The first term of a geometric sequence is 300 and the common ratio is 0.6. What is the 7th term of the sequence? 13.9968 4. What is the 15th term of the sequence 4, –8, 16, –32, 64 ? 65,536 Holt McDougal Algebra 1

9-1 Geometric Sequences Lesson Quiz: Part II Find the next three terms in each geometric sequence. 5. The table shows a car’s value for three years after it is purchased. The values form a geometric sequence. How much will the car be worth after 8 years? Year Value ( ) 5570.39 1 2 3 Holt McDougal Algebra 1 18,000 15,300 13,005